高校大学生分类管理中基于等价类的属性约简算法应用

Application of Attribute Reduction Algorithm Based on Equivalent Class in Classification Management of College Students

摘要: 本文针对高校大学生群体的特殊性，提出利用形式概念分析进行学生分类管理，为学生工作者提供有价值的参考依据。将属性特征与等价类的方法应用于属性约简，提出了属性约简的判定定理并予以证明；其次提出属性约简及输出算法，首次将属性约简算法应用于高校大学生分类管理，具体做法是：根据属性建立二叉树，调用前序、中序及后序遍历，得到相应序列，首先删掉一个属性，再将每个概念的内涵与剩余属性求交集，若求交集的结果均为单元素集，则该属性可约，否则跳过该属性，重复以上步骤，可以得到约简集；随后讨论了算法的时间复杂度，本文首次将约简集输出算法的时间复杂度降为多项式级。通过实例分析，对比了其它属性约简算法的运行效率和分类能力，证明本文提出的算法具有可行性和正确性。最后进行了总结并讨论了开放性问题。

Abstract: Based on the particularity of the college student group, this paper proposes to use formal concept analysis for classification management of students, which provides valuable reference for student workers. This paper applies characteristics of attribute and equivalent class to attribute reduction, puts forward judging theorems of attribute reduction with demonstration; secondly, proposes an algorithm of attribute reduction and output, applies this algorithm to classification management of college students for the first time. Specifications are as follows: first of all, establish a binary tree with attributes and obtain sequences of PreOrder, InOrder and PostOrder; delete an attribute; then perform intersection between the rest of attributes and each intent of concepts gradually, if each result contains single element, then this attribute can be removed, otherwise, skip this attribute, repeat the procedures above, consistent set can be obtained, reduction set which involves the minimum elements of consistent set can be output as well; subsequently, discusses the time complexity, this paper reduces the time complexity of reduction set output to polynomial level for the first time. Comparing with other algorithms on runtime and ability of classification, experi-mental results show that the proposed method approves feasibility and accuracy, in the end, draws a conclusion and discusses open issues.

1. 引言

1966年，克拉克(Clark)和特罗(Trow)从大学认同度(identification with college)和参与思想(involvement with ideas)两个维度将学生分为4类，分别为：学术型(academic)、社交型(collegiate)、职业型(vocational)、不墨守成规型(nonconformist)；李志峰 [1] 把学生分为高度匹配型、独立型、被动顺应型和排斥型等几种类型，按照学生的不同类型形成多样化和更为自主性的管理范式，有利于调动学生学习积极性，促进学生成长成才成功。国内研究大部分是以学生成绩、学习行为等依据进行分类，这种分类关注的是学习结果，忽视了其他影响因素。学生分类管理，不能简单以学习成绩为依据，学习成绩好并不一定思想行为就没有问题，分类管理的意义在于引导学生认识到一个真正优秀的人应该尽可能各方面都变得优秀。这才是正确的教育过程。

学生中的特殊群体理应成为学生工作者关心的重点对象。一般地，我们可以将学生中的特殊群体分为以下几类：行为障碍类学生、情绪化类学生、学习困难型学生。行为障碍类学生通常会表现出攻击行为、破坏行为，他们极度自我，不服从管理，这类学生经常打架，通过打架证明自己的价值；情绪化类学生通常表现为缺乏安全感，他们经常感到恐惧、抑郁，解决问题往往会采取极端的方法，极易出现心理问题；导致学习困难的原因有很多，比如学生可能沉迷于网络，可能因为早恋，也可能受原生家庭的影响，导致这类学生可能上课听讲很认真，但是就是学不会，还可能存在厌学倾向，因为学不会而放弃学习。学生很可能属于上述两种甚至是三种类型。有关分类的方法李珍 [2] 利用数据挖掘分析工具K-means聚类分析方法，对河北农业大学商学院2016年新生入学成绩进行了分析。结果表明，由于学生自身特点不同，即便是总分相差不多的情况下，在单科成绩上并不均衡，建议根据不同学生的学业特点，建立学生学业分类管理系统。不难发现，简单的分类方法易给学生带来敏感的情绪，分类指导的效果并不理想。本文尝试利用形式概念分析对学生进行分类管理，以期为学生工作者提供更有效的参考依据。

形式概念分析 [3] 最早由德国教授Wille R.提出，以形式背景和形式概念为基础，开创了概念格理论与应用研究的先河。随后形式概念分析作为一种数据和知识处理的有效工具，已被广泛应用于机器学习、模式识别、数据挖掘、计算机推理、知识发现等领域。

随着形式背景中数据的增多，基于形式背景的概念数量会急剧增加。因此建立有效的概念格构造算法及属性约简算法成为研究的热点。

马垣 [4] 等人研究了减少多个属性的一次性渐减式概念格构造算法，该算法与减少单个属性的渐减式算法有相同的时间复杂度，但当，减少多个属性时，单属性的渐减式算法需要反复执行多次，而该算法只需执行一次；李进金等人 [5]，通过引入交式可约元的概念，给出了基于可约元的概念格生成算法。

国外学者针对属性约简的主要研究方向有两个：基于粗糙集的知识约简和利用不可辨识矩阵的属性约简。Skowron教授 [6] 提出了基于区分矩阵的求核算法，为今后对区分矩阵进行合取、析取运算，求出形式背景的属性约简打下坚实的基础；Sabita Mahapatra [7] 等利用粗糙集理论及不可辨识矩阵进行属性提取并抽取出了决策规则，并与统计方法进行了对比。

国内学者主要以概念格属性约简为研究热点，概念格属性约简在保持形式背景中所有概念的外延集不变的前提下，寻找极小属性子集，该属性子集依然能够完全确定形式背景上的原有概念，并保持它们之间原有的层次结构关系。

王霞等人 [8] 主要研究了基于不可约元的概念格的属性约简以及属性约简集的构造，提出了一种概念格的属性约简方法；王璨 [9] 等人通过设定阈值将模糊形式背景转换为经典形式背景，给出约简集的判定定理，提出了属性约简及相对必要属性组合的输出算法；莫京兰 [10] 等对信息系统进行分布式处理，将子系统的核与约简合并得到原系统的核与约简；徐怡 [11] 等人结合粒计算思想，提出基于属性分类的形式概念属性约简模型，定义两个算子来划分属性之间分类关系，提出基于属性分类的形式概念约简算法，减少了冗余计算和存储开销上述文献开创了属性约简研究的先河；Xiuyi Jia [12] 等人定义了同一决策类中的对象的类内相似度以及不同决策类之间对象的类间相似度。其次，通过最大化类内相似度和最小化类间相似度定义基于相似度的属性约简粗糙集模型。在考虑启发式搜索策略的基础上，设计了一个属性约简方法，实验结果表明文中提出的算法能够提高分类的性能。

上述文献都具有很好的参考价值，但针对高效的属性约简集的输出算法研究较少，算法的运行效率也不高。因此本文以高效的属性约简集输出算法为研究重点。

本文分为五部分：第一部分介绍了概念格的相关理论；第二部分引入了属性约简的相关理论并对属性约简的判定定理予以证明；第三部分提出了基于等价类的属性约简算法并分析了算法的时间复杂度；第四部分通过实验分析，证明本文提出的算法具有可行性与正确性；最后，对本文进行了总结并讨论了开放性问题。

2. 概念格理论基础

形式背景被记为一个三元组 $\left(X,Y,I\right)$ ，其中X是有限的对象集，Y是有限的属性集， $I\subseteq X\times Y$ 是一个二元关系， $I\left(x,y\right)\in \left\{0,1\right\}$ 。

定义1 令 $A\subset X$ ， $B\subset Y$ ，则：

$A^{\ast }=\left\{y|\forall x\in A,I\left(x,y\right)=1\right\}$

$B^{\ast }=\left\{x|\forall y\in B,I\left(x,y\right)=1\right\}$

$A^{\ast }$ 是对象集A共同具有的属性集， $B^{\ast }$ 是共同具有属性集B的对象集。 $\langle A,B\rangle$ 是一个概念当且仅当 $A=B^{*}$ 且 $B=A^{*}$ 。其中A为概念的外延，B为概念的内涵。

性质1 $A^{\ast }=\underset{x\in A}{\cap }{x}^{\ast }$ ， $B^{\ast }=\underset{y\in B}{\cap }{y}^{\ast }$ .

性质2 $Y_1\subseteq Y_2\subseteq Y\Rightarrow Y_2{}^{\text{*}}\subseteq Y_1{}^{\text{*}}$ 。

性质3 $Y_1\subseteq Y_1{}^{\text{**}}$ 。

证明：由概念的外延和内涵的定义可证。

偏序关系( $\le$ )可以描述概念间的等级结构。 $\langle A_1,B_1\rangle$ 和 $\langle A_2,B_2\rangle$ 是形式背景 $\left(X,Y,I\right)$ 下的两个概念， $\langle A_1,B_1\rangle \le \langle A_2,B_2\rangle$ 当且仅当 $A_1\subset A_2$ 或 $B_1\supset B_2$ 。

若 $B\subseteq B_1$ 并且没有 $\langle A_2,B_2\rangle$ 满足 $B\subseteq B_2\subseteq B_1$ ，则 $\langle A_1,B_1\rangle$ 是 $\langle A,B\rangle$ 的后继。

概念格 [13] [14] [15] [16] [17] 是偏序集，概念格中的每个元素拥有最小上界和最大下界。基于形式背景 $\left(X,Y,I\right)$ 的概念格记为： $L\left(I\right)=\left(\left(X,Y,I\right),\le \right)$ 。

定理1 $\forall a\in Y$ ， $\langle a^{\ast },a^{\ast \ast }\rangle$ 为概念。

证明：令 $A=a^{\ast }$ ， $B=a^{\ast \ast }$ ，则 $B=A^{\ast }$ ； $B^{\ast }=a^{\ast \ast \ast }=a^{\ast }=A$ ，满足概念的定义，证毕。

推论1 $Y_1\subseteq Y$ ， $\langle Y_1^{\ast },Y_1^{\ast \ast }\rangle$ 为形式概念。

推论2 $X_1\subseteq X$ ， $\langle X_1^{\ast \ast },X_1^{\ast }\rangle$ 为形式概念。

证明：由定理1和外延内涵的定义及性质易证。

3. 属性约简相关理论

定义2对于概念格 $L\left(I\right)=\left(\left(X,Y,I\right),\le \right)$ ， $\forall \langle A,B\rangle \in L\left(I\right)$ ， $\exists \langle C,D\rangle \in L\left(I_1\right)$ ，使 $A=C$ ，则称 $L\left(I_1\right)$ 细于 $L\left(I\right)$ 。

若 $L\left(I_1\right)$ 细于 $L\left(I\right)$ 且 $L\left(I\right)$ 细于 $L\left(I_1\right)$ ，则 $L\left(I_1\right)$ 与 $L\left(I\right)$ 同构，记为 $L\left(I_1\right)\cong L\left(I\right)$ 。

定义3 [18] 令 $\left(X,Y,I\right)$ 为形式背景，若存在属性集 $E\subseteq Y$ 使得 $L\left(I_E\right)\cong L\left(I\right)$ 。则称E为形式背景的协调集，进一步地 $\forall e\in E$ ，满足 $L\left(I_{E-e}\right)$ 与 $L\left(I\right)$ 不同构，则称E是形式背景的约简，所有的约简集记为 $E_i$ .

定义4 [4] 令 $E\subseteq Y$ ，则E上的等价关系定义为： $R_E=\left\{\langle A,B\rangle ,\langle C,D\rangle |\langle A,B\rangle ,\langle C,D\rangle \in L\left(I\right),B\cap E=D\cap E\right\}$ 。则称 $L\left(I\right)/R_E$ 为E确定的等价类。

易证 $R_E$ 为等价关系。

定义5 各等价类中的最大元素定义为： $\left\{\langle A,B\rangle |\forall \langle C,D\rangle \in L\left(I\right),B\cap E=D\cap E,C\subset A\right\}$ 。

从定义5可知，等价类中的最大元素为该等价类中位于概念格中层次最高的概念。

定理2 [4] E上的子背景 $\left(X,E,I_E\right)$ 中的概念 $\langle A_1,B_1\rangle$ 满足E确定的某个等价类中的最大元素 $\langle A,B\rangle$ ，使 $A_1=A,B_1=B\cap E$ 。

证明见文献 [4]。

定理3 若E确定的等价类的个数为N，其中N为 $L\left(I\right)=\left(\left(X,Y,I\right),\le \right)$ 中概念的个数，且各等价类均为单元素集，则E为形式背景 $\left(X,Y,I\right)$ 的协调集。进一步删除E中属性，直至E确定的等价类不全为单元素集，则E为约简。

证明：已知E确定的各等价类均为单元素集，即各等价类中的最大元素即为该单元素，由定理2可知，每个单元素与子背景中的概念一一对应，又因为单元素的个数与原始背景中的概念个数相同，且外延不变，所以，概念格的结构保持不变，满足协调集的定义，进一步删除协调集中的属性至子概念格与原概念格不同构，满足属性约简的定义，得证。

由定理2、3可知，属性约简的问题将转化为判断等价类是否为单元素集的问题。

形式背景中的属性可以分为三类 [6]：

(1) 核心属性： $C=\cap E_i$ ，其属于每个约简。

(2) 相对必要属性： $J=\cup E_i-\cap E_i$ ，其属于某些约简但不属于每个约简。

(3) 不必要属性： $K=Y-\cup E_i$ ，其不属于任一约简。

定理4 $\forall a\in Y$ ，若 $a^{\ast \ast }=a$ ，则a为核心属性。

证明：由定理1可知， $\langle a^{\ast },a^{\ast \ast }\rangle$ 为概念，又因为 $a^{\ast \ast }=a$ ，则 $\langle a^{\ast },a\rangle$ 为概念，由协调集的定义可知，a为协调集中的属性，进一步地，若删除属性a，会导致删除前后的概念格不同构，所以a为每个约简集中的属性，即a为核心属性。证毕。

引理1 在等价关系R下， $R=\left\{\left(a,b\right)\in Y\otimes Y|a^{\ast }=b^{\ast }\right\}$ ，相对必要属性的划分为 $J/R=\left\{J_i|i=1,\cdots ,n\right\}$ ，E为该形式背景下的约简集，则 $\left|E\cap J_i\right|=1$ 。

证明详见文献 [8]。

定理5 C和J为形式背景下的核心属性集和相对必要属性集， $J/R=\left\{J_i|i=1,\cdots ,n\right\}$ ， $\forall E\subseteq Y$ ，E是形式背景的约简集当且仅当 $E=C\cup e_i\left\{e_i\in J_i|i=1,\cdots ,n\right\}$ 。

证明详见文献 [8]。

4. 属性约简算法

由以上论述可以归纳出基于等价类的属性约简算法的一般步骤：首先删掉一个属性，再将每个概念的内涵与剩余属性求交集，若求交集的结果均为单元素集，则该属性可约，否则跳过该属性，重复以上步骤，可以得到所有的协调集，元素个数最少的协调集即为约简集。下面以伪码形式给出基于等价类的属性约简算法：

(1) 根据属性构造二叉树，调用二叉树前序、中序、后序算法，得到前序、中序、后序属性序列。

(2) 生成条件概念：

输入：形式背景 $\left(X,Y,I\right)$ ；

调用概念生成算法；

输出：所有概念。概念的存储结构采用结构体数组 $C\left[N\right]$ ，N为概念的个数，C有四个成员，no存储内涵中元素的个数，数组 $E\left[\left|X\right|\right]$ 存储外延，数组 $I\left[\left|Y\right|\right]$ 存储内涵。

(3) 将核心属性，存入数组 $Core\left[\left|Y\right|\right]$ ：

for each $C\left[i\right]$

if( $C\left[i\right].no==1$ ) $i\to Core\left[\left|Y\right|\right]$ ;

(4) 等价类法进行属性约简，根据前序、中序、后序序列，调用以下算法三次：

{E=Y;

for (i=1; $i\le \left|Y\right|$ ; i++)/*从第i个属性开始，依次判断属性 $Y\left[i\right]$ 是否可删*/

{if ( $Y\left[i\right]$ in $Core\left[\left|Y\right|\right]$ ) continue;/*核心属性不能约*/

$E=E-Y\left[i\right]$ ;/*将去掉属性 $Y\left[i\right]$ 后的剩余属性存放于E中*/

for each $C\left[j\right]$

{k=0;

$s\to data=E\cap C\left[j\right].I\left[\left|Y\right|\right]$ ;/*将剩余属性E与每个概念的内涵求交存入节点S的数据域，k为计数器，记录相交属性的个数*/

$s\to next=p\left[k\right]\to next$ ；

$p\left[k\right]\to next=s$ ;}/* $p\left[k\right]$ 为指针指示相交后有k个属性的单链表，采用头插法插入每个结点*/

k=0;

while( $p\left[k\right]\to next$ )/*比较各非空的单链表*/

{ $q=p\left[k\right]\to next$ ;

p=q;

while( $q\to next$ )

{ $p=p\to next$ ;

while(p)

if( $p\to data==q\to data$ ) break;/*两个结点的数据域相等，说明该等价类不是单元素集，则剩余结点无需比较*/

else $p=p\to next$ ;

if(p!=NULL) break;

$q=q\to next$ ;

p=q;

}

if( $q\to next$ ) break;

k++;

}

if( $k<N$ ) $Y\left[i\right]\to E$ ;/*不能约，存入数组E*/

}

算法的时间复杂度分析：

概念的生成算法最优可以在线性的时间下完成 [19]，在一般情况下，具有最优时间复杂度的概念生成算法之一是Ganter提出的算法，每个概念为。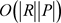

不难发现步骤(3)等价类法属性约简的时间复杂度主要耗费在求交集与比较各单链表是否有两个结点的数据域相等，复杂度分别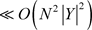，，所以本文的算法时间复杂度。

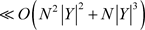5. 实验分析

例1形式背景如表1所示，概念详见表2，生成的概念格如图1所示。

为了说明算法的正确性，仅举从删a开始的约简过程：

前序序列为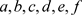，中序序列为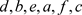，后序序列为。下面以前序序列为例，说明算法的步骤。

Table 1. Formal context

表1. 形式背景

Table 2. Generated concepts

表2. 生成的概念

Figure 1. The concept lattice

图1. 概念格

(1)

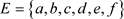
(2)，删a，因为a不是核心属性，所以

(3) 依次求交集，得到各单链表：；；；；；；

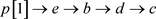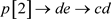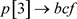(4) 各单链表中无相同元素，所以开始删b，因为b不是核心属性，

(5) 依次求交集，得到各单链表：；；；；；

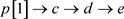(6)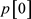中存在相同元素，所以b不能删，；

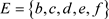(7) 因为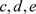是核心属性，所以结束本次循环；

(8) 因为f不是核心属性，所以；

(9) 依次求交集，得到各单链表：；；；；；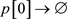

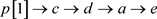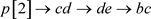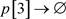(10) 各单链表中无相同元素，最终输出约简。

同理，可得另外一个约简。

为了更好地说明本文的算法效果，我们在硬件配置为CPU E6600，内存2GB的计算机上，操作系统为Windows 10，采用 Microsoft Visual C++ 6.0作为运行环境，我们选取3组随机的形式背景进行实验，实验结果表明随着形式背景中数据的增多，算法的执行时间会有所提高，执行效率不如文献 [20] 提出的约简算法高，但与文献 [9] (时间复杂度为中算法的运行效率相比，本文提出的算法运行效率更高，具体如图2所示。

Figure 2. The efficiency

图2. 运行效率

概念格属性约简的前提是寻找极小属性子集，该属性子集依然能够完全确定形式背景上的原有概念，并保持它们之间原有的层次结构关系。为了说明本文算法的有效性，约简后的形式背景见表3，得到的概念见表4，不难发现，约简前后的概念数量和概念格的结构均没有发生改变，证明了本文算法的有效性。

另外，属性约简前后属性对对象的分类能力也不应改变。为了更好地说明本文算法的分类能力，我们选取文献 [9] 的例子进行对比，结果表明两种约简算法均能保证约简前后属性的分类能力不变，但本文的算法对约简的输出效率更高，详见表5。

现将本文算法应用于学生分类管理的实例中，学生分类数据如表6所示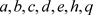，分别表示心理问题、学习困难、上网成瘾、谈恋爱、家庭困难、暴力倾向、个性强，生成的概念详见表7，具体过程见表8，最终输出约简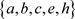。其目的在于，虽然去掉了谈恋爱和个性强两个属性，但学生的分类不变，能够将学生管理者有限的时间和精力放在最为重要的观测点上，便于学生管理者采取有针对性的措施进行干预，如建立学生帮扶共进小组等，能够较大幅度提高学生管理的针对性和效率。

Table 3. Formal context after reduction

表3. 约简后的形式背景

Table 4. Concepts after reduction

表4. 约简后的概念

Table 5. Comparison with ability of classification

表5. 分类能力比较

Table 6. Another context

表6. 另一个形式背景

Table 7. Generated concepts

表7. 生成的概念

Table 8. Procedures of reduction

表8. 约简过程

6. 结束语

本文利用等价类法进行属性约简，并设计出了运行效率较高的约简集输出算法，丰富了概念格属性约简的研究理论，借助单链表结点s、结构体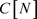数组、指针数组等存储结构，巧妙地设置循环控制条件(continue)，本文提出的属性约简算法的时间复杂度，与输出相对必要属性组合相比，时间复杂度从指数级降为多项式级。将算法创新性地应用于学生分类管理中，输出约简集的子集能够为学生工作者提供更有效的参考依据。

属性约简集输出算法仍然依赖于相对必要属性等价类的个数，其组合情况和属性的排列情况有关，若考虑属性的所有排列情况，又会使算法的运算级别升为阶乘级。因此如何设计更高效的属性约简集输出算法是文章进一步的研究方向。

致谢

在此衷心感谢论文撰写过程中各位作者的通力支持，同时对参考文献中作者的工作表示诚挚地感谢。

基金项目

辽宁省自然科学基金项目(2019-ZD-0349，2019-ZD-0348)。

NOTES

^*通讯作者。