基于传递矩阵法的充液管道振动功率流计算分析

Calculation and Analysis of Vibration Power Flow in Liquid-Filled Pipes Based on Transfer Matrix Method

摘要: 针对管路系统中的流固耦合振动问题，采用Riccati传递矩阵法计算了一段管路的振动特性和振动功率流，获得了管路系统的振动固有频率以及位移谐响应结果，并与有限元仿真结果进行了对比，进一步分析了振动功率流沿管路的传递分布，最后研究了弹性支撑刚度和阻尼对振动功率流的影响。计算结果表明，采用本文方法计算管路的振动特性具有一定的准确性，振动输入功率流沿着管路传递逐渐衰减，在弹性支撑处会有明显的衰减，并且其考虑了响应的幅值和相位差，在振动评价中更加准确和全面。

Abstract: Aiming at the fluid-structure coupling vibration problem in the pipeline system, the Riccati transfer matrix method is used to calculate the vibration characteristics and vibration power flow of a section of pipeline. The vibration natural frequency and displacement harmonic response results of the pipeline system are obtained, and the results were compared with finite element simulation. The transmission distribution of the vibration power flow along the pipeline was further analyzed. Finally, the influence of the stiffness and damping of the elastic support on the vibration power flow was studied. The calculation results show that the calculation of the vibration characteristics of the pipeline using the method in this paper has a certain accuracy. The vibration input power flow is gradually attenuated along the pipeline, and there will be obvious attenuation at the elastic support. Since vibration power flow takes the magnitude and the phase difference into account, it is more accurate and comprehensive in vibration evaluation.

1. 引言

管道作为一种典型的质量流、能量流、动量流输送系统，在众多行业内都有着不可替代的重要应用。管路系统在被广泛使用的同时，也不可避免的会出现各种问题，其中最具有代表性的就是充液管道的流固耦合振动问题。管路系统的振动能量会随着管内流体和管壁传递到管路系统的各个位置，再进一步地通过连接件由管路系统传递给与之相连的系统，一方面会造成管路结构薄弱处和精密元器件的破坏，影响管路系统的正常运行，严重时会导致巨大的经济损失 [1]；另一方面振动还会降低工作人员的环境质量，对声隐身性能有要求的舰船也有着严重的威胁。

刘红梅 [2] 基于周期结构理论，计算了无限长的圆柱壳振动功率流，分析了几个重要的结构参数对振动功率流的控制效果，并进一步以圆柱壳的输入功率流为控制目标函数，采用主动力方式对圆柱壳的振动功率流进行主动控制；赵文俊 [3] 采用有限元法，建立了飞机“机体结构–支撑组件–液压管路”机械振动模仿真型，基于有限元功率流理论，对液压管路系统的能量传递路径进行了分析和识别，并进一步通过实验验证了其结果的准确性；姚煜中 [4] 基于Hamilton原理，采用有限元法建立了管路系统的流固耦合振动模型，并对管路系统的振动功率流进行了计算和分析，说明了以功率流为振动评价指标的优越性。丁旭 [5] 针对一段飞机的空间管路系统，采用有限元功率流法结合传递路径分析方法，计算分析了其振动能量的分布和传递。

本文以一段典型的管路为例，基于管路流固耦合振动的经典十四方程，首先采用Riccati传递矩阵法计算了管路流固耦合的振动模态和响应，并与ANSYS仿真对比验证了该方法的准确性。其次对管路的振动功率流进行了计算分析，研究了管路振动功率流沿管路的传递和分布规律，说明了振动功率流与振动响应之间的区别与联系，最后对不同弹性支撑的刚度和阻尼对振动功率流的影响进行了分析。

2. 管路流固耦合RICCATI传递矩阵法理论

管路系统流固耦合振动的传递矩阵模型已经在文献 [6] 中有详细推导，其基于铁木辛柯梁理论，考虑管路的泊松耦合，选取管路的位移、转角、力和弯矩以及流体的压强和流速为状态变量来描述各自的运动状态，根据结构振动力学和流体力学原理，通过管壁处的边界相容条件，建立管路系统的流固耦合运动方程，进而求解运动方程得到管路的传递矩阵模型，其中弯管模型的建立采用了离散的思想，将弯管简化为多个具有一定夹角的短直管连接而成，De Jong [7] 在其研究中指出连续模型和离散模型的求解结果基本一致，并且对于求解小曲率弯管的振动特性，连续性模型没有优势。本文由于篇幅原因不再赘述，只是在上述基础上，引入Riccati变换提高传递矩阵的数值计算的精度和稳定性。

Riccati传递矩阵法采用的计算模型和传统传递矩阵法没有任何区别，只是在求解上有差异，并且前者在保留了后者所有优点的基础上，大大提高了计算的数值稳定性、准确性以及效率 [8]。

对于第i个管路单元左(L)右(R)两侧的无量纲状态变量有如下表达式：

${\left[\bar{\Phi }\right]}_i^R=\left[\bar{T}\right]{\left[\bar{\Phi }\right]}_i^L+{\left[\bar{f}\right]}_i$ (1)

式中 $\left[\bar{\Phi }\right]$ 是该段管路的无量纲状态变量， $\left[\bar{T}\right]$ 为无量纲传递矩阵， $\left[\bar{f}\right]$ 是无量纲的载荷列向量。

Riccati变换首先将状态变量分为管路起点已知和未知两类，通常这两类各占一半，并将传递矩阵也做相应的划分：

${\left[\begin{array}{c}{\bar{\Phi }}_a\\ {\bar{\Phi }}_b\end{array}\right]}_i^R=\left[\begin{array}{cc}{\bar{T}}_{11}& {\bar{T}}_{12}\\ {\bar{T}}_{21}& {\bar{T}}_{22}\end{array}\right]{\left[\begin{array}{c}{\bar{\Phi }}_a\\ {\bar{\Phi }}_b\end{array}\right]}_i^L+{\left[\begin{array}{c}{\bar{f}}_a\\ {\bar{f}}_b\end{array}\right]}_i$ (2)

式中 ${\bar{\Phi }}_a$ 是管路起点处状态向量已知的一半元素， ${\bar{\Phi }}_b$ 则是另一半的元素， ${\bar{T}}_{11}$ 、 ${\bar{T}}_{12}$ 、 ${\bar{T}}_{21}$ 和 ${\bar{T}}_{22}$ 则是将传递矩阵 $\bar{T}$ 中的元素重新进行排列后形成的子矩阵， ${\bar{f}}_a$ 是载荷列向量 $\bar{f}$ 中与 ${\bar{\Phi }}_a$ 对应的元素组成的列向量， ${\bar{f}}_b$ 则是载荷列向量 $\bar{f}$ 中与 ${\bar{\Phi }}_b$ 对应的元素组成的列向量。

引入如下Riccati变换：

${\left[{\bar{\Phi }}_a\right]}_i={\left[S\right]}_i{\left[{\bar{\Phi }}_b\right]}_i+{\left[e\right]}_i$ (3)

上式将同一管道截面上的已知状态变量 ${\bar{\Phi }}_a$ 与未知状态变量 ${\bar{\Phi }}_b$ 建立起联系，待定的 ${\left[S\right]}_i$ 称为当前节点处的Riccati传递矩阵， ${\left[e\right]}_i$ 是与载荷相关的列向量。

将展开可以得到

${\left[{\bar{\Phi }}_a\right]}_i^R={\left[{\bar{T}}_{11}\right]}_i{\left[{\bar{\Phi }}_a\right]}_i^L+{\left[{\bar{T}}_{12}\right]}_i{\left[{\bar{\Phi }}_b\right]}_i^L+{\left[{\bar{f}}_a\right]}_i$ (4)

${\left[{\bar{\Phi }}_b\right]}_i^R={\left[{\bar{T}}_{21}\right]}_i{\left[{\bar{\Phi }}_a\right]}_i^L+{\left[{\bar{T}}_{22}\right]}_i{\left[{\bar{\Phi }}_b\right]}_i^L+{\left[{\bar{f}}_b\right]}_i$ (5)

将式(3)代入式(4)和式(5)中，并联立消去 ${\left[{\bar{\Phi }}_a\right]}_i^L$ 和 ${\left[{\bar{\Phi }}_b\right]}_i^L$ 可得

${\left[{\bar{\Phi }}_a\right]}_i^R={\left[S\right]}_{i+1}{\left[{\bar{\Phi }}_b\right]}_i^R+{\left[e\right]}_{i+1}$ (6)

式中

${\left[S\right]}_{i+1}=\left({\left[T_{11}\right]}_i{\left[S\right]}_i+{\left[T_{12}\right]}_i\right){\left({\left[T_{21}\right]}_i{\left[S\right]}_i+{\left[T_{22}\right]}_i\right)}^{-1}$ (7)

${\left[e\right]}_{i+1}={\left[T_{11}\right]}_i{\left[e\right]}_i+{\left[{\bar{f}}_a\right]}_i-{\left[S\right]}_{i+1}\left({\left[T_{21}\right]}_i{\left[e\right]}_i+{\left[{\bar{f}}_b\right]}_i\right)$ (8)

上述两个式子便得到了 ${\left[e\right]}_i$ 和 ${\left[S\right]}_i$ 的一般递推关系式，若管路系统被分为n个管单元，那么计算时首先根据管路起点出的边界条件直接得出 ${\left[e\right]}_0$ 和 ${\left[S\right]}_0$ 的值，逐渐递推直至算出管路终点处的 ${\left[e\right]}_{n+1}$ 和 ${\left[S\right]}_{n+1}$，再代入式 中便可以得到终点处未知的状态变量，最后依次回代便得到各个节点处的状态变量，具体方法详见文献 [9]。

3. 管道振动特性计算

如图1所示的充水管路，由直管、弯管、弹性支撑和集中质量组成，每一段的管长以及坐标系均已在图中标明，管道为铜管材料，密度为8900 kg/m³，泊松比为0.32，考虑材料的阻尼系数为 $\eta =0.005$，即复杨氏模量为 $E=1.08\times {10}^{11}\times \left(1+0.005i\right)\text{Pa}$，管道截面内半径为r = 0.024 m，壁厚为e = 3e−3 m；水的密度为998.2 kg/m³，体积模量为1.42e5Pa；弯管部分为直角，弯管半径为0.2 m，三向弹性支撑刚度为 $k_x=k_y=k_z=\text{1e6}\text{N}/\text{m}$，阻尼为10 N∙s/mm；管道一端固支，液体封闭，另一端管道和液体均自由。在管路的自由端加载三向的单位简谐激励力 $F_x=F_y=F_z=\text{1}\text{N}$，采用Riccati传递矩阵计算方法，在1~200 Hz内以1 Hz为步长扫频计算该结构的固有频率和谐响应。

Figure 1. Pipeline calculation model

图1. 管路计算模型

分别通过本文方法和有限元仿真计算管路系统的固有频率得到其前五阶如表1所示。其中有限元仿真模型采用ANSYS建立，管路采用Beam188单元模拟，弹性支撑采用Combin14单元模拟，流体以附加质量的形式均布在管壁上。对比可以发现两者的误差比较小，均在5%以内，可以看出本文方法具有较高的计算精度。

Table 1. The natural frequencies of the piping system

表1. 管路系统固有频率

进一步计算其x方向的位移幅值响应如图2所示，从图中可以看出，两者方法计算得到的位移幅值响应吻合的比较好，由此可见本文计算的方法计算的准确性。

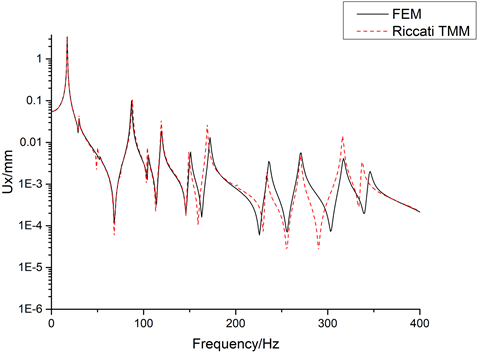
Figure 2. Comparison of the displacement amplitude response of the two methods in the x direction

图2. 两种方法x方向位移幅值响应对比

4. 管道振动功率流计算

4.1. 振动功率流定义

在物理学中功率是描述物体做功快慢的物理量，其定义为单位时间内所作功的大小，类似的对于振动而言，振动功率流其反映的是振动波单位时间内传播的能量 [9]。以梁的轴向振动为例，设梁上某一点处的轴力为：

$F_z=F_0{\text{e}}^{j\omega t}$ (9)

设轴向振动速度与轴力的相位差为 $\phi$，则速度可以表示为：

$V_z=V_0{\text{e}}^{j\left(\omega t+\phi \right)}$ (10)

管道轴向振动的能量流定义为一个周期内振动能量的平均值，其表达式为：

$P_{Fz}=\frac{1}{T}{\displaystyle {\int }_0^T\mathrm{Re}\left(F_z\right)\cdot \mathrm{Re}\left(V_z\right)\text{d}t}=\frac{1}{2}{F}_0{V}_0\cos \phi =\frac{1}{2}\mathrm{Re}\left(F_z{V}_z^{\ast }\right)$ (11)

式中 $V_z^{\ast }$ 表示 $V_z$ 的共轭，Re表示取实部。在简谐激励的作用下，速度与位移有着如下关系：

$V_z=j\omega U_z$ (12)

为方便计算功率，将(12)代入(11)中，可以得到功率与位移与力的表达式：

$P_{Fz}=\frac{1}{2}\mathrm{Re}\left(F_z{V}_z^{\ast }\right)=\frac{1}{2}\mathrm{Re}\left(-j\omega F_z{U}_z^{\ast }\right)$ (13)

类似的可以得到弯矩的功率为：

$P_{Mz}=\frac{1}{2}\mathrm{Re}\left(-j\omega M_z{\psi }_z^{\ast }\right)$ (14)

综合x、y、z三个方向后，可得整个管道的总功率为：

$P=P_{Fx}+P_{Fy}+P_{Fz}+P_{Mx}+P_{My}+P_{Mz}$ (15)

对于输入到管道的总功率，一部分通过自身的阻尼作用耗散掉，一部分则通过连接件传递给了其它构件。同样的，对于输入到每个管段上的功率，一部分用于自身的振动，最后由阻尼逐渐消耗掉，另一部分则传递给了相邻的元件，因此对于每个管段的输入功率有：

$P_{in}=P_{out}+P_{damp}$ (16)

事实上对于无阻尼的系统，由于没有阻尼消耗能量，即 $P_{damp}=0$，由(16)可知 $P_{in}=P_{out}$，也就是说输入到系统的功率等于系统输出的功率，因而作用在系统上的功率为0，所以计算结构的振动功率流时阻尼是必须要考虑的。

4.2. 振动功率流计算

根据上述对于管道振动功率流的定义，进一步对前文的管道系统进行功率流的计算。为了更加细致的展现功率流沿管路的分布，对于直管部分，取每段直管单元长度为0.1 m，将弯管部分化为8段短直管，这样便共有10 + 8 + 20 + 8 + 15 = 61个管段和62处位置(节点)的状态变量，其中节点6，24，34，52为弹性支撑的位置，节点62为外载荷功率输入点。

图3给出了管路系统三个方向的振动输入功率流级，振动功率级 $L_w=10\ast {\log }_{10}\left(P/P_0\right)$，其中基准功率为 $P_0=1.0\text{e}-1\text{2}\text{W}$。从图中可以发现y方向的功率流要略小于x方向的，而x、y方向的功率流则要明显大于z方向的，将200 Hz内的功率进行求和，计算得到三个方向200 Hz内的总功率分别为 $P_x=0.1597\text{W}$， $P_y=0.1285\text{W}$ 和 $P_z=0.0135\text{W}$，进一步证明了管路系统中的轴向振动要小于横向的弯曲振动。

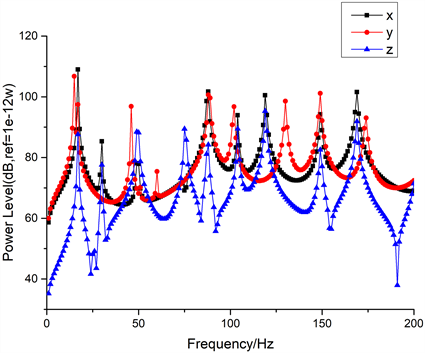
Figure 3. Three-direction input power flow level of piping system

图3. 管路系统的三方向输入功率流级

系统的总输入功率流级如图4所示，从图中可以看出，管路系统总输入功率和频响曲线类似。图中总输入功率流级的前三个峰值对应的频率为15、17和30 Hz，而通过对比表1中的系统振动固有频率发现，功率流出现峰值的频率点与固有频率有关，但并不是所有的固有频率处其振动功率都一定会出现峰值。

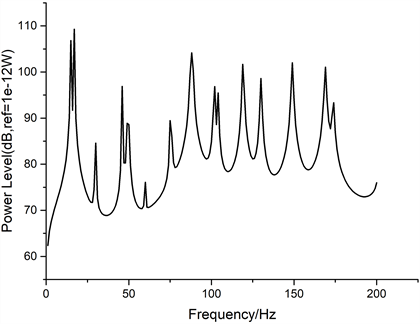
Figure 4. The total input power flow level of the pipeline system

图4. 管路系统的总输入功率流级

以力的功率为例，由式(13)容易得到其功率P的计算值为

$P=\frac{1}{2}\omega F_0{U}_0\sin \phi$ (17)

可见P与角频率 $\omega$ 、响应的幅值(力 $F_0$ 、位移 $U_0$ )以及相位差 $\phi$ 的正弦值成正比，而响应的幅值是与系统固有频率相关的。此外，从频响曲线中也可以看出随着频率的增高，系统的响应幅值是逐渐减小的，但是在图2系统总输入功率图上并没有这种趋势，这也是因为P还与角频率 $\omega$ 成正比。综合以上分析可以看出，以功率流作为振动的评价指标，比直接用振动响应要更加全面，其次功率作为一种统一的度量，在某一频带内或者不同位置处的功率都可以进行简单的线性叠加，并且结果都有其明的确物理意义，这也是采用振动响应无法做到的。

图5为四个支撑处的输入功率流级，由图可以看出离载荷最近的支撑4处输入功率流最大，离载荷越远，输入功率流就越小，这是因为每一个管段都在消耗能量，能量在沿管道传递过程中不断损耗。

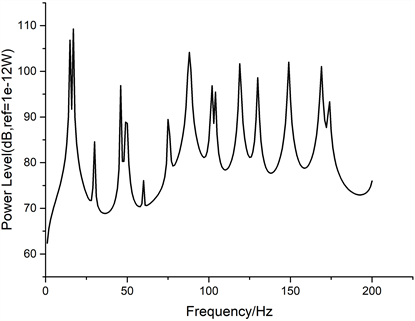
Figure 5. Input power flow at elastic support

图5. 弹性支撑处的输入功率流

为进一步分析功率流沿着管路的分布，这里取频率为20 Hz时，计算每个管单元节点处的输入功率流，得到如图6所示的功率流分布图，其中第一个节点处的功率流为0，因为图中取了对数坐标，故无法显示在图上。从图中可以看出，沿着管路系统远离载荷的方向，各管段的输入功率流逐渐降低，其中在节点52、34和24处，功率流有着非常明显的陡降，这是由于弹性支撑的缘故，经过计算节点52处降低了2.66e−05W，节点34处降低了2.67e−06W，节点24处降低了1.25e−06W，由此可见第4个弹性支撑处阻尼消耗了最多的能量，进一步观察可以发现其实第1个支撑处也有一定的降低，只是不够明显，约降低了8.2e−08W。

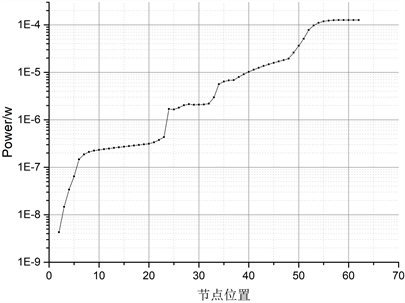
Figure 6. Distribution of vibration power flow along the pipeline at 20 Hz

图6. 20 Hz时振动功率流沿管路的分布

4.3. 弹性支撑对振动功率流的影响

4.3.1. 弹性支撑刚度

分别取弹性支撑刚度为1e5 N/m、5e5 N/m和1e6 N/m时，计算其200 Hz内的输入功率计算结果如下图所示，从图7中可以看出刚度对振动的输入功率流的频谱特性影响较大，但是在一定的刚度范围内对功率流的幅值大小影响较小。

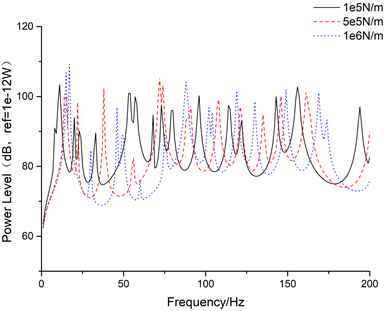
Figure 7. Input power spectrum of pipeline system under different stiffness

图7. 不同刚度下管路系统输入功率频谱

此外，若刚度增加到一定程度，则弹性支承处效果接近固支，那么输入功率流在第一个支撑处便降为0。这里取弹性支撑刚度为1e15 N/m计算其20 Hz时输入功率流的传递，得到图8所示的曲线，计算发现在经过第一个支撑(节点52)后功率流已经降到1e−40级别(图中仅标注到1e−20)，基本上等于0，后续的功率流计算已经超出数值计算精度，故未展示。可以发现图中结果与上述分析是一致的。

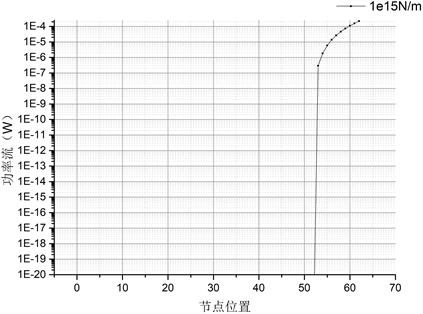
Figure 8. Input power flow transfer when the stiffness is 1e15 N/m

图8. 刚度为1e15 N/m时的输入功率流传递

4.3.2. 弹性支撑阻尼

为研究弹性支撑的阻尼对输入功率的影响，分别取10、50和100 N*s/mm计算系统的输入功率流，结果如下图9所示。从图中可以看出阻尼越小，系统的输入功率越小，这与极端情况下阻尼为0时，系统的输入功率为0是一致的。

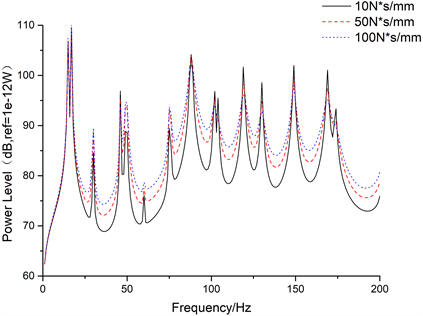
Figure 9. Input power flow under different elastic support damping

图9. 不同弹性支撑阻尼下的输入功率流

下图10为20 Hz时，管路系统输入功率流沿着管路的传递分布，从图中可以看出输入功率随阻尼的增大而增大，但是在弹性支撑处的损耗也逐渐增大。

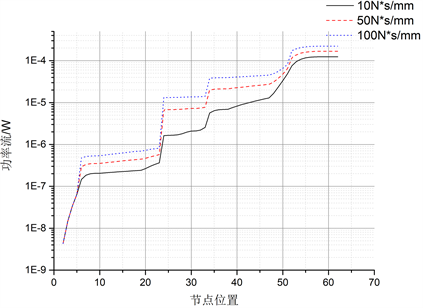
Figure 10. Power flow distribution under different damping

图10. 不同阻尼下的功率流分布

5. 结论

本文基于经典的管路系统流固耦合振动十四方程组，采用Riccati传递矩阵法计算分析了一段管路的振动特性和功率流的分布，通过有限元仿真的对比，验证了本文方法的准确性；管路功率流的大小与管路系统的固有频率相关，但是并不是所有的固有频率处都会出现功率流的峰值，功率流综合考虑了三个方向的力、位移、弯矩和转角的大小，并且还考虑了各自的相位差，因此在振动评价中具有更加全面和准确的优势；比较200 Hz内的总功率流，可以发现管路系统轴向的振动要小于横向的弯曲振动；弹性支撑的刚度过大时，会直接阻断功率流沿着管路的传递；弹性支撑的阻尼增大，管路系统的输入功率也会增大，但相应的位置处阻尼消耗的能量也会增大。

基金项目

国家自然科学基金资助项目(51839005, 51879113)；中央高校基本科研业务费资助项目 (2019kfyXMBZ048)。

NOTES

^*通讯作者。