动车组风笛发声仿真方法研究

Research on Simulation Method of EMU Air Whistle Sound

摘要: 动车组风笛的鸣笛声是保证铁路安全高效运营的重要听觉信号。铁道行业标准对动车组风笛各项技术指标有严格规定，而动车组导流罩隔声会导致风笛外声场声压级降低。为保证风笛能够安全有效地传递信号，对风笛发声的进行准确地数值仿真显得十分重要。本研究根据风笛工作原理，采用流固耦合分析方法，对于高压气流激起膜片振动的过程进行模拟仿真，得到风笛出口处压力变化曲线。用有限元方法对风笛鸣笛声在外声场传播过程进行模拟仿真，研究预测风笛外声场的声压级分布。建立了风笛试验测试系统，测试得到在不同工作风压下规定测点产生的总声压级(A计权)和基频，测试结果与仿真结果吻合，验证了本研究仿真方法的准确性。

Abstract: The sound of EMU air whistle is an important auditory signal to ensure safety and efficient operation of railway. The railway industry standards strictly stipulate various parameters of air whistle for locomotives and EMU, but sound insulation of shroud reduce the sound pressure level of external sound field. In order to ensure that air whistle can transmit signals safely and effectively, it is very important to accurately simulate the sounding process of it. Based on working principle of air whistle, Fluid-Structure-Interaction analysis method is used to simulate the process of diaphragm vibration produced by high-pressure air flow, and then the pressure change curve at the air whistle outlet is obtained. The propagation process of air whistle in external sound field is simulated by finite element method, and then the external sound field distribution is predicted. An air whistle test system is established to test the total sound pressure level (A-weight) and frequency of the air whistle under different working air pressures, which further verified the accuracy of the fluid-structure interaction and the external sound field simulation method.

1. 引言

动车组的风笛声是铁路运行时的重要声信号，具有突发性、声级大、传播范围广的特点，同时已成为影响铁路沿线声环境的重要噪声源。在噪声预测的过程中，需要明确风笛的源强参数，包括强度参数以及指向性参数 [1]。风笛作为动车组发声装置，其工作原理为：初始时风笛膜片与喇叭喉部接触闭合，当空气进入风笛腔内导致腔内气压升高，推动膜片产生形变并与风笛喇叭喉部脱离接触，腔内空气由喇叭喉部进入喇叭口，腔内气压降低，膜片恢复形变，喇叭口接近闭合状态。空气继续进入腔内，腔内气压再次升高，如此往复，膜片振动发出声音。膜片振幅决定鸣笛声的声压级，膜的振动结构和流体对膜片的附加质量影响鸣笛声的频率。

王磊、李元齐、沈祖炎 [2] 通过数值计算和实验研究了附加质量对薄膜振动特性的影响。饶明航、潘毅等人 [3] 建立了薄膜气弹性模型，并根据膜结构特殊性进行简化处理，采用流固耦合方法进行分析，结果显示附加质量通过改变膜的振动结构来影响薄膜振动过程，当来流的风速增加时，薄膜振动的附加质量增大，造成振幅增加且频率减小。冯舰锐、陈聪等人 [4] 制作了膜片在长管中振动的结构模型，研究分析了管子尺寸和薄膜密度等参数对膜片型风笛发声频率的影响。林鹏、赵艳菊等人 [5] 建立头车的几何模型，并输入风笛的技术参数，采用Virtual.lab声学间接边界元方法，对于风笛发出的远场声压进行了仿真分析，得到的仿真结果与实验结果基本一致。Zheng Huang、Ying Xiong [6] 等人将大涡模拟(LES)湍流模型引入瞬态双向流固耦合仿真，对柔性水翼进行了仿真计算，得出激励源为湍流脉动，作用在结构上的压力幅值以及频率。

2. 声学及流、固体动力学理论

风笛是由膜片振动发生，振动激励来源为高压空气和膜片间的相互作用，高压空气推动膜片导致膜片产生位移和形变，而膜片的位移和形变也会反作用于流体域，影响流体的压力速度分布。因此在研究风笛工作过程时，需要考虑膜片的振动过程、流固耦合作用以及声音在流场传播过程。

2.1. 膜的振动及声学原理

在张紧的平面膜上，膜片微元受力变形图如图1所示，该面元的运动方程可以根据牛顿第二定律得出 [7]：

$T\left(\frac{{\partial }^2\eta }{\partial x^2}+\frac{{\partial }^2\eta }{\partial y^2}\right)\text{d}x\text{d}y=\sigma \text{d}x\text{d}y\left(\frac{{\partial }^2\eta }{\partial t^2}\right)$ (1)

式中，T代表张力(在整个膜上为常值)； $\eta$ 为膜上一点相对初始位置的法向位移，单位N/m； $\sigma$ 为面密度，代表膜的单位面积质量； $\sigma \text{d}x\text{d}y$ 代表面元的质量。

经过整理可得

${\nabla }^2\eta =\frac{1}{c}\frac{{\partial }^2\eta }{\partial t^2}$ (2)

式中， $c=\sqrt{\frac{T}{\sigma }}$， ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ 为二维直角坐标坐标系下的Laplace算符，式(2)即为膜的振动方程。

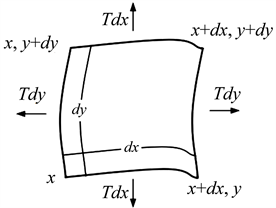
Figure 1. The diagram deformation caused by external force

图1. 膜片微元受力变形图

在本文所研究的风笛，是由圆形膜片振动发声，所以将平衡方程由直角坐标系向极坐标系转换。这时，在极坐标下的圆膜振动方程可表示为

$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial }{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^2}{\partial \theta }=\frac{1}{c^2}\frac{{\partial }^2\eta }{\partial t^2}$ (3)

式中r为极径； $\theta$ 为极角。

而当圆膜振动时，位移 $\eta$ 与极角 $\theta$ 无关，则方程可简化为

$\frac{{\partial }^2\eta }{\partial r^2}+\frac{1}{r}\frac{\partial \eta }{\partial r}=\frac{1}{c^2}\frac{{\partial }^2\eta }{\partial t^2}$ (4)

当气体推动膜片从风笛腔内进入喇叭口时，薄膜受力可视为表面均布载荷，则其振动方程可表示为：

$T\left(\frac{{\partial }^2\eta }{\partial x^2}+\frac{1}{r}\frac{\partial \eta }{\partial r}\right)+P-P_0={\sigma }_c\frac{{\partial }^2\eta }{\partial t^2}$ (5)

式(5)中， ${\sigma }_c\left(\text{kg}/{\text{m}}^{\text{2}}\right)$ 为薄膜等效面密度； $P_0\left(\text{Pa}\right)$ 为标准大气压。

由于膜片形变对整个腔内空间大小的影响相对较小，可以忽略不计，并假设因气流造成的附加质量在膜上均匀分布。则有

$\pi r^2\sigma +m_a=\pi r^2{\sigma }_c$ (6)

由于风笛腔内的气压分布受输入风压、空腔体积、薄膜属性影响，同时气压是随时间变化的且与上一时刻的气压分布相关，因此很难准确地获得附加质量数值并求解出腔内气压与时间的关系。根据现有研究结果，不同的边界条件、计算模型以及模型理想化程度对于附加质量的计算结果影响很大，因此本文在之后研究中使用流固耦合的方法来分析风笛膜片振动对流体压力的影响。

2.2. 流固耦合理论

为解决流致振动问题，需要根据流固耦合特性将求解过程分成流体域求解、固体域求解以及流固耦合面上的数据交换三个部分 [8]。

2.2.1. 流体控制方程

流体流动要遵循质量守恒定律、动量守恒定律以及能量守恒定律，三个物理学上的基本守恒定律 [9]。对于一般的可压缩流体，可根据基本守恒定律列出以下控制方程。

质量守恒方程：

$\frac{\partial {\rho }_f}{\partial t}+\nabla \cdot \left({\rho }_{f}v\right)=0$ (7)

动量守恒方程：

$\frac{\partial {\rho }_{f}v}{\partial t}+\nabla \cdot \left({\rho }_{f}vv-{\tau }_f\right)=f_f$ (8)

其中，t表示时间， $f_f$ 是体积力矢量。 ${\rho }_f$ 是流体密度，v是流体速度矢量， ${\tau }_f$ 是剪切力张量，可表示为：

${\tau }_f=\left(-p+\mu \nabla \cdot v\right)I+2\mu e$ (9)

其中，p是流体压力， $\mu$ 是动力粘度，e是速度应力张量， $e=\frac{1}{2}\left({\nabla }_v+{\nabla }_v^{\text{T}}\right)$

2.2.2. 固体控制方程

固体部分的守恒方程可以由牛顿第二定律导出：

${\rho }_s{\ddot{d}}_s=\nabla \cdot {\sigma }_s+f_s$ (10)

其中， ${\rho }_s$ 是固体密度， ${\sigma }_s$ 是柯西应力张量， $f_s$ 是体积力矢量， ${\ddot{d}}_s$ 是固体域当地加速度矢量。

2.2.3. 流固耦合方程

流固耦合同样遵循最基本的守恒原则，在流固耦合交界面处，应满足流体与固体应力、位移、热流量、温度等变量相等和守恒，即满足如下4个方程：

$\{\begin{array}{l}{\tau }_f\cdot n_f={\tau }_s\cdot n_s\\ d_f=d_s\\ q_f=q_s\\ T_f=T_s\end{array}$ (11)

为便于分析，通常会建立控制方程的通用形式，然后输入各参数并设置适当的初始和边界条件，统一求解。目前，用于解决流固耦合问题的方法主要有两种：直接耦合式解法和分离解法。直接耦合式解法通过把流固控制方程耦合到同一方程矩阵中求解，在理论上非常先进和理想。但是，在实际应用中，直接解法很难将现有CFD (computational fluid dynamics)和CSM (computational structural mechanics)技术真正结合到一起，同时考虑到同步求解的收敛难度和耗时问题，本文研究采用分离解法进行计算。分离解法是分别求解流体控制方程和固体控制方程，再把流体求解和结构求解的计算结果在耦合面上传递交换。当这一时刻的计算完成时，再对下一时刻求解，依次而行得到最终结果。

3. 风笛膜片的流固耦合仿真

本研究根据风笛膜片的结构和工作原理，分别对风笛流场和固体结构进行建模并划分网格。导入ANSYS Workbench进行流固耦合仿真计算，得到流场的压力分布、固体域的形变等重要参数，并可将计算所得流场出口处的空气压力、速度等随时间变化的参数作为后续外声场仿真分析的输入参数。

3.1. 风笛流体有限元模型

首先在SolidWorks 中建立风笛内流场部分的几何模型，导入Hypermesh进行几何清理。因为流体模型中存在狭窄缝隙和相对宽阔区域，而且气流管道结构比较复杂，所以本研究中采用四面体非结构化网格对流体域进行分块划分。风笛膜片与喉部间距为0.003 mm，为流体域内最小间隙，为保证结果精确，薄膜至少应在法线方向上划分三层网格。风笛气流管路入口处结构尺寸较小，划分网格尺寸小于等于2 mm，喇叭口内划分网格尺寸小于等于5 mm。划分完成得到有限元模型如图2所示，包含2,291,191个网格单元。根据流固耦合仿真计算的要求对网格质量进行检查，为保证计算结果准确，网格质量应大于等于0.3 [10]。经检查，流体模型网格质量小于0.3的网格不超过0.1%，满足流固耦合仿真要求。

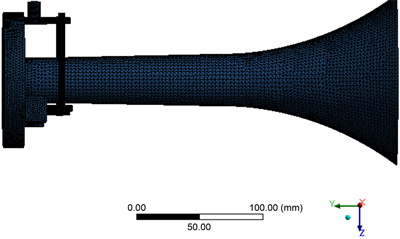
Figure 2. The finite element model of fluid domain

图2. 风笛流体有限元模型

设置流体属性为空气，采用RNG k-eplion湍流模型，定义边界条件，设置入口压力和出口压力。本文研究的风笛工作气压范围为0.6~1.0 MPa，初始压力小于等于0.2 MPa。风笛内空气为亚音速流动，通过边界流体单元压力值外插获得静压值。压力入口处的气流速度由理想气体等熵关系式计算得到，再根据流动方向矢量得到入口处的速度分量。通过理想气体状态方程计算流体域中的气体密度。气流入口处压力通过自定义函数方式进行设置，在0.001秒内压力由0.2 MPa提高至0.75 MPa，之后保持0.75 MPa稳定状态。压力出口设置为0 Mpa。

由于流固耦合的仿真计算中流场边界可能会随结构运动而变化，并且该变化对于流场计算影响不可忽略，因此需要在计算过程中不断更新流体网格 [11]。本研究仿真的动网格更新方法设置为弹簧光顺以及局部网格重构。

3.2. 风笛固体有限元模型

本文研究的风笛，其振动发声的主要结构为膜片，因此只需对膜片和相关安装固定结构进行建模仿真研究。建立膜片和其固定结构模型，包括厚度为0.5 mm的圆形弹簧钢膜片以及3.4 mm环状橡胶垫。对模型进行网格划分得到固体域有限元模型如图3，单元数量为21119，单元类型为六面体单元。膜片结构部分材料为弹簧钢，网格类型为SOLID185单元，密度为7850 kg/m³，杨氏模量为2.06 × 10¹¹ Pa，泊松比为0.3；固定结构材料为橡胶，网格类型为HYPER58，定义为Mooney-Rivlin超弹性本构模型，参数设置中C10为0.6915 MPa，C01为0.1372 MPa，不可压缩常数D1取值为0.001，密度为1300 kg/m³。

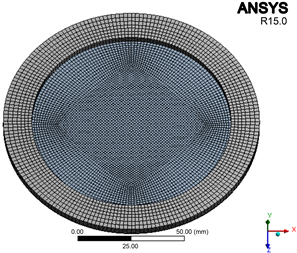
Figure 3. The finite element model in solid domain

图3. 固体域有限元模型

为了便于在流固耦合仿真时设置求解步长和时长，先对建好的膜片振动结构模型进行模态仿真计算，得到整个结构1~6阶模态频率如表1所示。

Table 1. The 1st-6th frequency of diaphragm vibration structure

表1. 膜片振动结构的第1~6阶频率

在ANSYS Workbench的TransientStructural模块中，在振动结构对应位置设置固定约束，在膜片背面设置数值为一个大气压的表面压力载荷。将膜片与风笛喇叭喉部接触面设为流固耦合面，并监测膜片上位移数值。具体设置如图4所示。

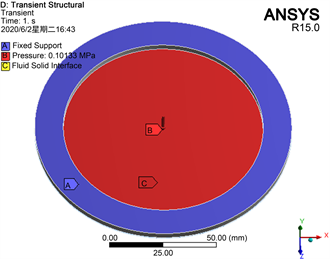
Figure 4. The boundary condition setting in solid domain

图4. 固体域边界条件设置

为了提高膜片流固耦合仿真的准确性，确保求解过程中动态网格更新时不会产生负体积或者过高畸变率的网格，需要调整步长进行多次尝试计算。最终在System Coupling模块设置的耦合求解总时长围0.01 s，步长5 × 10⁻⁵ s，步数为200。设置完毕后进行计算求解。

3.3. 流固耦合仿真结果分析

流固耦合仿真计算完成后，分别得到了流体域和固体域的计算结果，分析输入压力为0.75MPa时风笛流体域的压力和固体域的位移结果，及其随空间、时间变化情况。

3.3.1. 固体域结果分析

图5是膜片在输入气压为0.75 MPa情况下膜片中心点的位移随时间变化曲线图，从图中可以看到t = 0.00205 s时刻，膜片中心点位移达到最大值，t = 0.003 s时刻，位移最小。从图6中可以看出，膜片进行稳定振动后，膜片中心处位移最大，其位移最大值为0.566 mm，最小值为0.149 mm。

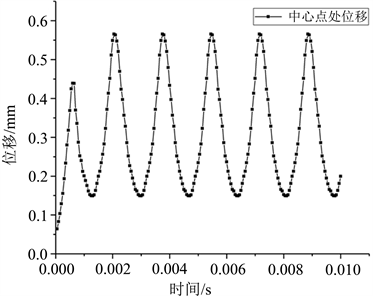
Figure 5. Displacement curve at the center of the diaphragm

图5. 膜片中心点处位移变化曲线

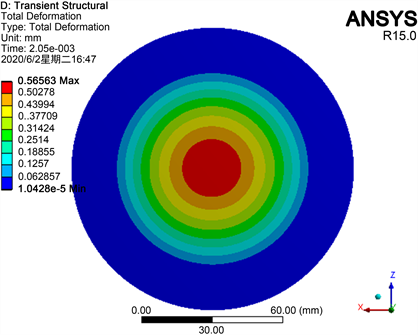
Figure 6. Diaphragm deformation at the maximum displacement of diaphragm Center

图6. 膜片中心位移最大时变形情况

对图5中位移–时间曲线上的离散点进行快速傅里叶变换(FFT)，以获得膜片振动结构的频域分布。由于流固耦合计算时设定步长为5 × 10⁻⁵ s，采样点数较少，会因频率间隔较大而难以得到较为准确的频域分布情况，因此需要补充膜片稳定振动后的采样点数量。通过快速傅里叶变换后得到的膜片中心位移响应频谱如图7所示，可知风笛膜片发声时，其振动频率为617.5 Hz，与1阶模态频率626.46 Hz的数值接近。

Figure 7. Displacement response spectrum at the center of the diaphragm

图7. 膜片中心点处位移响应频谱

3.3.2. 流体域结果分析

在t = 0.00205 s，即膜片中心位移最大时，风笛流体域压力分布情况如图8所示。此时出口面上中心点、1/2半径处和边缘处，压力值分别为103,796.32 Pa、103,773.65 Pa和103,725.69 Pa。

由图8可以看出，高压空气由入口经管道进入风笛腔，再推开膜片从腔内进入喇叭口，沿空气流动方向压力依次显著下降。风笛腔内压力分布均匀，是由于三通管道对腔内气压保持均匀起到很好的作用。风笛喇叭口内，由喉部到出口空气压力较小且分布均匀，气流流速较慢。

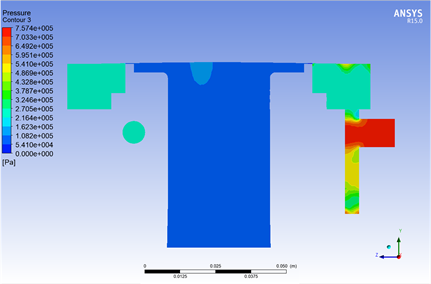
Figure 8. Fluid pressure distribution at the maximum displacement of diaphragm Center

图8. 膜片中心位移最大时流体域压力分布

在t = 0.003 s时刻，即膜片中心位移最小时，出口面上中心点、1/2半径处和边缘处，压力值分别为98,815.78 Pa、98,803.16 Pa和98,787.47 Pa。

在耦合面上，压力由流体域向固体域传递，当膜片位移到达最大时，耦合面上的压力同时达到最大。在t = 0.00205，即膜片中心位移最大时，耦合面压力分布如图9所示。在风笛腔体内的耦合面压力相对较高，最大值为527,633.56 Pa，呈环状均匀分布。在喇叭喉部区域的耦合面压力较低，最小值为29,430.74 Pa，呈圆形分布。

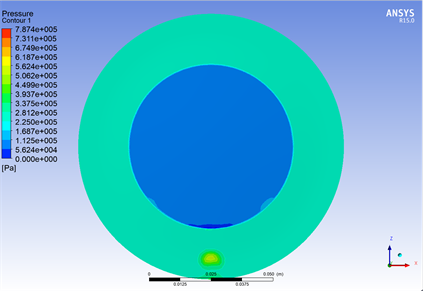
Figure 9. Interaction surface pressure distribution at the maximum displacement of diaphragm Center

图9. 膜片中心位移最大时耦合面上压力分布

图10(a)是风笛气流出口处中心点压力随时间的变化情况，在风笛达到稳定振动后，压力的最大值为103,796.32Pa，最小值为98,815.78 Pa。图10(b)是由图10(a)中离散点经快速傅里叶变换得到的出口中心压力频谱，该处压力变化频率为615.2 Hz，同膜片振动频率617.5 Hz近似相等。

(a) 出口中心点处压力时间曲线 (b) 压力频谱

Figure 10. Pressure at outlet center point

图10. 出口中心点压力变化

4. 风笛的外声场分析以及实验验证

4.1. 风笛的外声场仿真分析

完成流固耦合仿真计算和分析后，得到风笛气流出口压力时间关系和频率，可以此作为输入参数进行外声场仿真计算。根据《TB/T3051.2-2016》标准规定，在测试动车组风笛进行声压级时，声级计的传声器应置于风笛5 m的相同高度处进行测量。因此建立半径为5 m的半球形外声场，并划分网格建立声场有限元模型如图11。在外声场球心与风笛气流出口对应处划分的网格，应与流固耦合仿真中出口处流体网格相匹配，便于将风笛出口压力施加于此处作为激励声源。

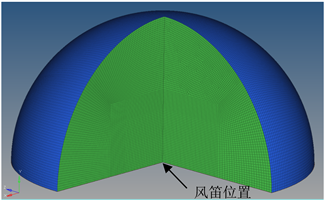
Figure 11. Sectional view of the air whistle external sound field finite element model

图11. 风笛外声场有限元模型剖面图

在Fluent中设置瞬态求解，流体属性设为空气。根据风笛气流出口压力时间曲线编写UDF文件，并设置为球心风笛位置的压力入口条件；设置外声场其他部分边界条件；在外声场内距球心0.625 m、1.25 m、2.5 m和5 m处设置多个监测点。设置完毕进行仿真计算。

在t = 0.00205 s，即风笛气流出口处压力最大时，过球心与半球底面垂直的截面压力分布情况如图12。

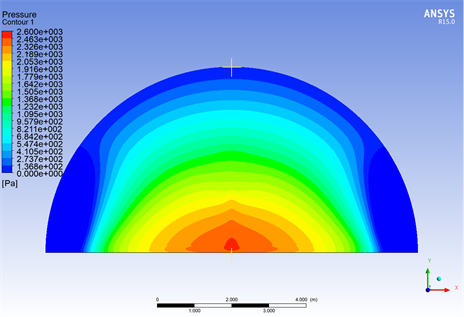
Figure 12. Pressure distribution in the external sound field of air whistle

图12. 风笛外声场压力分布情况

将风笛正前方距外声场球心0.625 m、1.25 m、2.5 m和5 m处监测点分别编号分别为1、2、3、4号测点。在与风笛正前方向夹角45˚延长线上，距外声场球心5 m位置设置监测点5。根据这5个监测点的压力结果进行计算分析。

以4测点为例，仿真结果得到风笛正前方5 m处有效声压 $P_e=18.64\text{Pa}$。

声压级计算公式如下：

$L_p=20\lg \frac{P_e}{P_{ref}}$ (12)

其中， $P_e$ 为有效声压， $P_{ref}$ 为参考声压， $P_{ref}=2\times {10}^{-5}\text{Pa}$。

则4测点处的声压级可有公式(12)计算得到，为119.39dB。根据《GB/T 3785.1-2010》，风笛工作频率下的A计权可由下式计算：

$A\left(f\right)=20\lg \left[\frac{f_4^2{f}^4}{\left(f^2+f_1^2\right){\left(f^2+f_2^2\right)}^{\frac{1}{2}}{\left(f^2+f_3^2\right)}^{\frac{1}{2}}\left(f^2+f_4^2\right)}\right]-A_{1000}$ (13)

式中，f为风笛工作频率，根据前文仿真结果可知其值为615.2 Hz， $f_1=20.60\text{Hz}$， $f_2=107.7\text{Hz}$， $f_3=737.9\text{Hz}$， $f_4=12194\text{Hz}$，归一化常数 $A_{1000}$ 为−2 dB。

计算得615.2 Hz的A频率计权为−2.03 dB。因此风笛正前方5 m处声压级为117.36 dBA。

其它位置测点根据仿真结果进行相同的数值计算，具体结果如表2所示：

Table 2. The sound pressure level calculation result of the external sound field

表2. 风笛外声场声压级计算结果

根据仿真结果的压力分布图与声压级数值计算结果可知，风笛外声场分布声压级由球心声源处向边缘递减，同时风笛声源具有明显的指向性，在标准测点声压级为117.36 dBA，而在45˚等距位置声压级为115.99 dBA，声压级差为1.37 dBA。

4.2. 风笛的外声场实验验证

通过仿真得到外声场声压级分布后，为了验证仿真结果的准确性，需要对该型动车组风笛进行声压级和频率测试。按照《TB/T3051.2-2016》标准规定，对于动车组风笛，应将风笛模拟安装在动车组上的相同高度，并在距风笛前方5m的相同高度位置上测量其声压级和频率。此次实验场地为半消声室，测点布置在风笛正前方5 m处以及左前方45˚延长线5 m处，如图13和图14所示。

Figure 13. The microphone is placed in front of the air whistle

图13. 传声器置于风笛前方测试

Figure 14. The test microphone is placed in air whistle 45˚ extension line

图14. 传声器置于风笛45˚延长线测试

4.3. 风笛测试结果和仿真结果对比分析

该型动车组风笛声压级和频率测试结果如表3所示：

Table 3. Air whistle test results

表3. 风笛测试结果

由表3可知在0.75 MPa的工作风压下，风笛鸣笛声频率为619 Hz，在标准测点(即正前方5 m等高处)的声压级为117.57 dBA，在45˚侧前方5 m处声压级为117.16 dBA。

风笛在输入风压为0.75 Mpa时，标准测点上仿真和测试的结果进行对比，如表4所示：

Table 4. The comparison between test results and simulation results

表4. 测试结果同仿真结果对比

在风笛外声场仿真计算中，正前方5 m等高处测点声压级为117.36 dBA，频率为615. 。在标准测点处仿真和实验声压级结果相差0.21 dBA，误差为0.18%，频率结果相差3.8 Hz，误差诶0.61%。实验测试结果与仿真计算结果基本一致，证明本文研究风笛发声和传播过程采用的仿真方法有效合理。

5. 结论

1) 本文根据风笛结构和工作原理，对于风笛膜片振动发声结构建模并进行模态分析，得到膜片的1~6阶模态频率，该结构1阶模态频率为626.4 Hz。

2) 建立风笛流体域和固体域的有限元模型，并用流固耦合方法进行仿真计算。得到在输入风压为0.75 MPa时，风笛内部流场的压力随时间分布，以及风笛膜片振动幅值和频率。风笛膜片在稳定振动时的频率为617.5 Hz；风笛气流出口中心点压力变化频率为615.2 Hz，与膜片振动频率基本一致。

3) 建立外声场有限元模型，将上一步仿真结果，即风笛气流出口处压力变化在外声场对应位置进行加载，计算出在标准测点处的声压级117.36 dBA。

4) 在半消声室中对动车组风笛外声场声压级进行实验测试，得到0.75 MPa输入风压下，标准测点处声压级和频率分别为117.57 dBA和619 Hz。与仿真结果基本吻合，证明本文研究的风笛发声仿真方法准确有效。

基金项目

中国国家铁路集团公司科技研究开发计划课题(P2019J008)。