碱金属热管传热特性的数值研究

Numerical Investigation on Heat Transfer Characteristics of Alkali Metal Heat Pipe

摘要: 碱金属热管以良好的传热性能被广泛应用于航天和核工等领域。含有吸液芯的碱金属热管的工作过程涉及高温环境下的相变和多孔介质流动等复杂物理现象。本文采用多孔介质模型和VOF模型对碱金属热管的工作过程进行数值模拟。采用用户自定义文件(UDF)编译蒸发–冷凝相变模型和毛细力模型。通过与前人实验数据进行对比验证了本模型的准确性。利用该模型分析了孔隙率和热流密度等参数对碱金属热管传热性能的影响。相同孔隙率下，热管的有效热阻随着热流密度的增大而减小。当热流密度相同时，热管的有效热阻随着孔隙率的增大而增加。

Abstract: With good heat transfer performances, alkali metal heat pipes are widely used in astronautics and nuclear engineering industries. Heat transfer of wicked heat pipe is related to processes of phase changes and porous medium flow with high operating temperature. In the current investigation, heat transfer of alkali metal heat pipe is simulated with porous media assumption and VOF model. The capillary force and the phase change process are compiled by User Defined Function (UDF). The numerical model is validated by experimental data in the literature. Based on the numerical model, heat flux effects and porosity effects on heat transfer performances of heat pipes are analyzed. With the same porosity, the effective thermal resistance is decreased with the increasing of heat flux. With the same heat flux, the effective thermal resistance is increased with the increasing of porosi-ty.

1. 引言

高温碱金属热管因具有等温性好和传热效率高等优点，被广泛应用在航天和核工等领域 [1]。图1是含有吸液芯的热管结构示意图。蒸发段内液体受热蒸发，高压蒸汽向冷凝段流动。蒸汽在冷凝段被冷却，发生冷凝。冷凝液体在吸液芯(丝网、泡沫金属等)毛细力的作用下回流至蒸发段。热管的工作过程涉及到流体相变、毛细力、多孔介质流动等多个复杂的物理过程。

Figure 1. Heat pipe geometry model

图1. 热管结构图

Thuchayapong等 [2] 采用有限元法(FEM)对二维稳态热管内的换热过程进行了数值模拟。采用线性函数描述气液交界面处的毛细半径，计算结果与实验数据吻合较好，并分析了毛细压力对热管性能的影响。Chang等 [3] 利用二维瞬态数值模型研究铜–水纳米流体热管的传热性能。结果表明纳米颗粒的加入降低了热管的壁温、工作压力、蒸汽温度和总热阻，从而提高了热管的传热性能。Alizadehdakhel [4] 利用VOF模型分析了热流和充液率对热虹吸管性能的影响。结果表明，每个热流值都有一个最优的充液率，过量增加热流反而会降低热虹吸管的传热性能。

Ali等 [5] 研究了吸液芯的孔隙率和渗透率对环形热管(Loop Heat Pipe，LHP)换热性能的影响。流动阻力随孔隙率的增加而增大，但是孔隙率过低无法提供足够的毛细压差。结果表明孔隙率在0.5~0.6时热管传热性能最佳。Mahjoub [6] 的数值结果表明圆柱热管的总热阻随芯孔隙率的增大而增大，随壁面导热系数和热管半径的增大而减小。Wang等人 [7] 分析了多孔材料的非均匀性对热管换热性能的影响。多孔材料的轴向梯度对传热和流动阻力的影响有限而径向梯度会显著地改变流体速度分布和流动阻力。因此，基于特定梯度的多孔材料配置可以实现传热性能和流体流动阻力的优化。Abdelaziz [8] 研究了多孔材料对竖直壁面凝结换热的影响。在竖直板上覆盖多孔层可以强化气液界面的传热传质过程。Singh等人 [9] 指出小孔径、高孔隙率、高渗透率的吸液芯可有效提高环形热管的换热特性。郑丽等人 [10] 对比了泡沫金属吸液芯和不锈钢丝网吸液芯对热管传热性能的影响。实验结果表明丝网热管具有良好的等温性能，但传热极限较低且其启动性能不如泡沫金属吸液芯热管。

Arab [11] 采用量纲分析方法研究了工质物性对梯形微槽道热管热阻的影响。发现热阻随工质导热系数和粘度的增加而增加，随表面张力、蒸发潜热和液体密度的增加而减小。Suman和Hoda [12] 研究了顶角，接触角等参数对V型热管性能的影响。热管的换热性能随截面顶角、倾角和热管长度的增加而降低，随表面张力和接触角的增加而提高。Suman和Hoda [12] 推荐选用表面张力高、粘度低、潜热容大、接触角大的冷却液。Savino等人 [13] 比较了纯水热管和水/醇二元混合物热管的传热性能。结果表明在较高的热流密度下，二元混合物热管的热阻较低。Wong等 [14] 研究了不同工质对双层烧结吸液芯平板热管换热性能的影响，采用不同工质热管的换热性能高度依赖于壁面热流密度。

曹小林等人 [15] 对脉动热管的通道结构进行改进，通过合理分配各通道内的流动阻力实现了工质在热管里的稳定单向流动。这种改进型脉动热管可以改善加热段的供液情况并提高热管传热性能。李玉华等 [16] 比较了热流密度、充液率和截面形状对脉动热管传热性能的影响。结果表明等腰直角三角形截面的脉动热管性能优于正三角形截面的热管。

以往研究大多假定气液相变发生在吸液芯–蒸汽腔的交界面上或者只发生在某一层特定的网格，并未模拟真实的相变过程。本文采用Fluent求解器中的多孔介质模型和VOF模型对碱金属热管的传热过程进行了数值研究。采用UDF编译Lee模型以模拟液态金属的蒸发–冷凝过程。毛细压力由Young-Laplace 方程计算，并通过UDF以动量源项的形式添加到动量方程中。通过与前人实验数据的对比，验证了模型的准确性。基于现有模型分析了孔隙率和热流密度对碱金属热管换热性能的影响。

2. 数值模型与方法

2.1. VOF模型

流体体积(VOF)方法，最初由Hirt和Nichols [17] 提出，可实现对气液界面的模拟。体积分数 ${\alpha }_i$ 为，

${\alpha }_i=\frac{i相体积}{总体积},{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i=1}$ (1)

VOF模型中流体物性为各相体积分数的加权平均。例如动力粘度系数 $\mu$ 和密度 $\rho$ 定义为，

$\rho ={\displaystyle \sum {\alpha }_q}{\rho }_q,\mu ={\displaystyle \sum {\alpha }_q}{\mu }_q$ (2)

2.2. 控制方程

连续性方程

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho V\right)=S_m$ (3)

其中 $S_m$ 为源项，用于模拟蒸发和冷凝过程中的质量传递。本文采用Lee模型计算该项。

动量方程 [18]

$\frac{1}{\epsilon }\left[\frac{\partial \rho V}{\partial \tau }+\nabla \cdot \left(\rho VV\right)\right]=-\frac{\partial p}{\partial x}+\frac{\mu }{\epsilon }\nabla \cdot \left(\nabla V\right)-\frac{\mu }{K}V-\frac{C_E}{\sqrt{K}}\rho \left|V\right|V-F_c$ (4)

$C_E$ 是Ergun系数， $F_c$ 是毛细力。 $\epsilon$ 是孔隙率，K是渗透率。

丝网吸液芯的孔隙率( $\epsilon$ )为 [19]，

$\epsilon =1-\left(\frac{1.05\pi N{d}_w}{4}\right)$ (5)

式中 $d_w$ 是不锈钢丝网的丝径，N代表丝网的目数。

渗透率(K)为 [20]

$K=\frac{d_{\omega }^2{\epsilon }^3}{122{\left(1-\epsilon \right)}^2}$ (6)

在蒸汽区，热管的孔隙率( $\epsilon$ )为1，渗透率接近无穷大( $K=\infty$ )，并且毛细力为零( $F_c=0$ )。此时，公式(4)与常规动量控制方程相同。

能量方程

$\frac{\partial \rho c_{p}T}{\partial \tau }+\nabla \cdot \left[\rho c_{p}VT\right]=\nabla \cdot \left(K_{eff}\nabla T\right)+S_E$ (7)

$K_{eff}$ 是多孔介质的有效导热系数，可以通过公式(8)计算得到 [21]

$K_{eff}=K_l\left[\frac{\left(K_l+K_s\right)-\left(1-\epsilon \right)\left(K_l-K_s\right)}{\left(K_l+K_s\right)+\left(1-\epsilon \right)\left(K_l-K_s\right)}\right]$ (8)

2.3. 毛细压力

热管工质循环的驱动力来自于毛细压差，因此最大毛细压差必须大于热管内所有压力损失的总和 [22]。热管中的压力损失主要分为沿蒸汽和液体流动路径的摩擦压降和相变导致的压降。

$\Delta p_c\ge \Delta p_{\text{tot}}=\Delta p_v+\Delta p_l+\Delta p_{\text{ph}}$ (9)

如果总压降超过最大毛细压差，则没有足够的驱动力促使液体回流到蒸发段进而导致蒸发段的吸液芯烧干，这就是热管的毛细极限。吸液芯中的毛细压力由Yang-Laplace方程(公式(10))计算 [23]

$\Delta P=\frac{2\sigma }{R_{\text{curve}}}=\frac{2\sigma }{r_{eff}}\cos \theta$ (10)

式中 $R_{\text{curve}}$ 为气液交界面曲率半径； $r_{eff}$ 是吸液芯有效孔半径； $\theta$ 是接触角，液态金属钠在不锈钢表面的接触角为15˚ [24]。丝网孔径与筛网数N有关 [23]。

$r_{eff}=\frac{1}{2N}$ (11)

2.4. 蒸发–冷凝模型

以往研究大多假定气液相变发生在吸液芯–蒸汽腔的交界面上 [3] 或者只发生在某一层特定的网格中 [25]。本文采用Lee模型 [26] 模拟相变过程，质量和能量源项如下式：

$S_m={\stackrel{\dot{}}{m}}_{lv}-{\stackrel{\dot{}}{m}}_{vl}$ (12)

$S_E=S_m\cdot h_{fg}$ (13)

$\{\begin{array}{l}{\stackrel{\dot{}}{m}}_{lv}=f_e\times {\alpha }_l{\rho }_l\left(T_l-T_{sat}\right)/T_{sat}\left(T_l>T_{sat}\left(\text{evaporation}\right)\right)\\ {\stackrel{\dot{}}{m}}_{vl}=f_c\times {\alpha }_v{\rho }_v\left(T_{sat}-T_v\right)/T_{sat}\left(T_v<T_{sat}\left(\text{condensation}\right)\right)\end{array}$ (14)

2.5. 几何结构与边界条件

本文通过与他人的实验数据进行对比 [25]，验证了该数值模型的准确性。表1给出了热管的具体几何参数，热管的尺寸和材料特性与实验参数一致。丝网物性和工质钾物性如表2所示 [27]。

Table 1. Parameters of the heat pipe

表1. 热管参数

Table 2. Thermophysical properties

表2.热物理性质

2.6. 有效热阻

有效热阻可表征热管换热性能。热管热阻的计算公式为

$R=\frac{T_e-T_c}{Q}$ (15)

Q为热管的热输入， $T_e$ 为热管蒸发段最高温度， $T_c$ 为热管冷凝段最低温度。

3. 结果与讨论

3.1. 模型验证

Sun等 [25] 测量了钾金属热管外壁温度在轴向的分布，并模拟了热管的换热过程。将本文的数值结果与Sun等 [25] 的实验数据和数值结果进行对比。对比结果如图2所示。将数值计算结果与相同轴向位置的测量温度进行比较，均方根误差为0.96%，平均相对误差为0.43%。模拟值与实验值吻合较好，验证了本文数值模型的准确性。

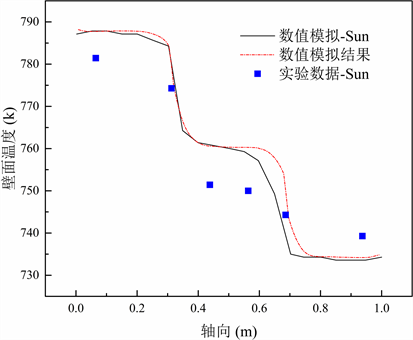
Figure 2. The simulated results compared with the reference [25]

图2. 模拟结果与参考文献进行比较 [25]

在以往的研究中，液膜的厚度被假定为常数，即气液交界面就是吸液芯与蒸汽腔的交界面。如图3体积分数云图所示，蒸发段液膜厚度小于绝热段和冷凝段液膜厚度，与实际工况相符。温度分布如图3所示，蒸发段和冷凝段径向温差大于绝热段。液体从冷凝段回流至蒸发段时，吸液芯中液体与热管内蒸汽不断进行换热，液体温度逐渐上升。

Figure 3. The volume fraction contours and temperature contours of the high-temperature heat pipe

图3. 高温热管的体积分数云图和温度云图

3.2. 热输入的影响

图4为不同热输入下的轴向壁面温度分布。蒸发段、冷凝段和绝热段温度呈现出阶梯状分布，绝热段与蒸发段，冷凝段的交界处温度梯度最大。如图4中标注所示，交界处的温度梯度随着热输入的增加而增加。最大温差随着热输入的增加而增加，当Q = 190 W时，蒸发段最高壁温为782.3 K，Q = 1140 W时，蒸发段最高壁温为806.5 K，即热输入增加到原来的6倍时，蒸发段最高壁温上升了24.2 K。

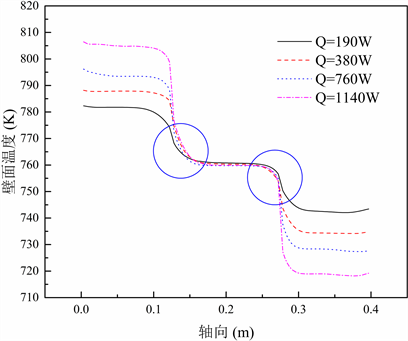
Figure 4. Axial wall temperature distribution with different heat input

图4. 不同热输入下热管壁面轴向温度分布

图5为不同热输入下热管热阻的计算值。热阻随着热输入的增加而减小。图中曲线的梯度可反映热输入对热阻的影响大小。热输入对热阻的影响随着热输入的增大而减小，与较低的热量输入相比，较高热输入下的热阻变化要小得多。

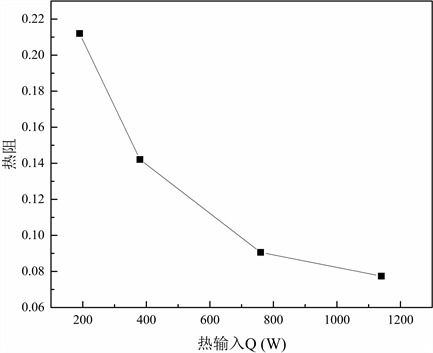
Figure 5. Variation of the thermal resistance with different heat input

图5. 不同热输入下热管的热阻

3.3. 孔隙率的影响

在相同的热输入(Q = 380 W)下，研究孔隙率分别为0.7，0.8和0.9时热管的传热性能。图6为不同孔隙率下热管的壁面温度分布。热管最大壁面温差随着孔隙率的减小而减小，即热管有效热阻随着孔隙率的减小而减小，因此较低孔隙率热管具有更好的等温性。

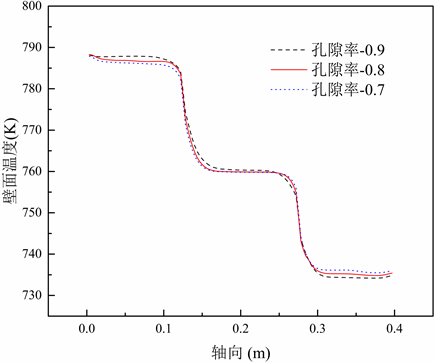
Figure 6. Axial wall temperature distribution with different porosity

图6. 不同孔隙率下热管轴向壁面温度分布

在热管蒸发段的轴向方向每隔10 mm选取1个截面，总共12个截面。计算每个横截面内液体的平均体积分数。图7为不同孔隙率下蒸发段液体体积分数分布。热管蒸发段的液体体积分数随着孔隙率的增加而增加，即说明孔隙率较低的热管蒸发段内的相变质量更大。在相同热输入下，相变带走的潜热越多，蒸发段显热越少。图8为热管蒸发段出口截面处的径向温度分布，孔隙率0.7的热管截面内流体温度最低，孔隙率为0.9的热管截面内流体温度最高。

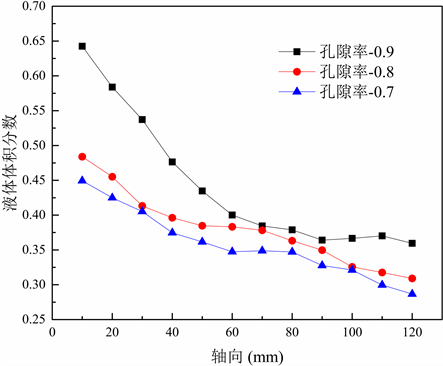
Figure 7. Volume fraction of liquid distribution in evaporation section with different porosity

图7. 不同孔隙率下热管蒸发段液体体积分数分布

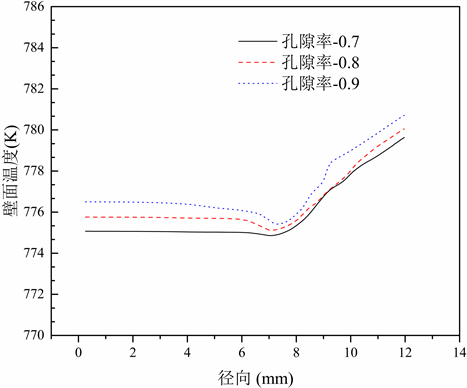
Figure 8. Radial temperature distribution at the exit of the evaporation section

图8. 蒸发段出口处径向温度分布

图9为不同孔隙率下热管冷凝段入口径向温度分布。图中椭圆为液膜区域温度分布。热管冷凝段蒸汽区域，流体温度随着孔隙率的增加而增加(除中心小部分区域外)。热管内温度越低，冷凝段内的蒸汽冷凝相变量越多，即冷凝段液膜越厚。

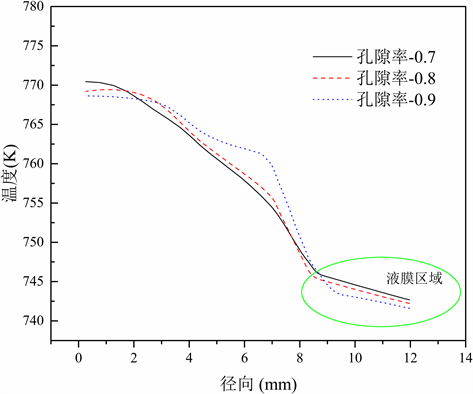
Figure 9. Radial temperature distribution at the entrance of the condensation section

图9. 冷凝段入口处径向温度分布

计算热管冷凝段不同截面处的液体体积分数，结果如图10所示。对于热管冷凝段的液膜厚度，孔隙率0.9的热管液膜最薄，孔隙率0.7的热管液膜最厚。

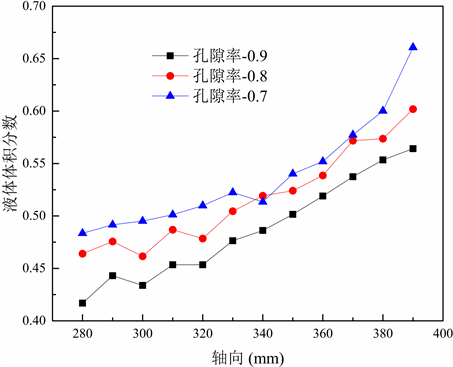
Figure 10. Volume fraction of liquid distribution in condensation section with different porosity

图10. 不同孔隙率下热管冷凝段液体体积分数分布

4. 结论

高温碱金属热管具有良好的换热性能，其工作过程涉及到金属相变和多孔介质流动等复杂过程。本文采用Fluent求解器中的多孔介质模型和VOF模型对碱金属热管的传热过程进行了数值研究。通过与前人实验数据的对比，验证了模型的准确性，并分析了孔隙率和热流密度对碱金属热管换热性能的影响。热管内不同轴向位置处的液膜厚度不同，且冷凝液体在回流至蒸发段的过程中与蒸汽换热导致其温度不断上升。热管热阻随着热输入的增加而减小。热输入下热阻的影响随着热输入的增大而减小。相同的热输入条件下，热管的热阻随着孔隙率的增加而增加。

基金项目

国家自然科学基金资助项目(No. 51906068)；中央高校基本科研业务费专项资金资助(2020MS032)。

NOTES

^*通讯作者。