1. 引言
航空发动机管路数量众多且结构复杂,管路之间一般通过管接头和卡箍等结构连接在一起,组成了各种管路系统结构。各种结构之间由于安装、焊接和相互耦合等原因,特别是由于机匣的强烈振动及温度、压力等外部环境剧烈变化的影响,管路系统经常会发生各种各样的振动故障,从而造成严重事故。管路系统结构的完整性对发动机的正常工作极其重要。目前,国内外学者对管路振动问题做了大量研究,Olson [1] 等采用梁单元为对象计算管道经常遇到的流固耦合问题。Mamaghani等 [2] 研究了非线性能量对输流管路在激励下的减振影响。卢丽金等 [3] 总结了飞机管路振动故障的机制和排除方法。李占营等 [4] 采用Galerkin方法研究了哥氏力和管路参数对航空发动机管路固有频率的影响。王世忠 [5] 等利用反对称矩阵理论计算方法对输液管道进行流固耦合问题分析。邱明星等 [6] 通过试验和数值计算结合的方法,验证了利用有限元方法计算充液管路固有频率的有效性的合理性。贾志刚等 [7] 通过研究对航空发动机的管路结构模式进行分类总结,基于结构参数分析了不同管路结构的振动特性。康力等 [8] 基于发动机试车数据,对典型管路的振动响应特性进行了计算。Qian Zhou等 [9] 针对航空发动机管道自动布线问题,提出了一种基于lee算法和遗传算法的新方法。Gholami Hojjat等 [10] 研究了循环内压作用下光滑凹痕或光滑凹痕与凿槽缺陷组合管道的应变基疲劳寿命分析。徐培原等 [11] 针对航空发动机外部管路系统卡箍布局不合理而导致发动机发生共振或振动过大问题,对发动机复杂管路的卡箍布局进行优化设计。航空发动机液压管路工作环境复杂,管路内部充满高压的液压油,外部发动机机匣的振动也会通过卡箍等紧固件对管路结构产生激励。刘玉柱等 [12] 有限元分析与振动应力测试相结合的方法,通过分析导管的固有频率和振动应力值,确定导管振动异常与外界激励影响有关,并提出了解决方案,当外激励和管路固有频率接近时产生共振,严重影响管路使用寿命。
本文基于ANSYSWork bench,对直管型管路、90˚型管路、S型管路、Ω型管路及其不同管路壁厚的航空发动机液压管路进行分析,为航空发动机外部管路的设计及优化提供依据。
2. 管路模型建立
2.1. ANSYS Workbench简介
ANSYS Workbench是一款功能强大的有限元仿真软件,软件内部集成了结构、流体、电场、磁场,声场等分析模块,各个模块之间也能实现耦合分析 [13] [14]。本文针对直管型管路、90˚型管路、S型管路、Ω型管路进行有限元仿真分析。
2.2. 管路有限元模型建立
模型材料为1Cr18Ni9Ti,其密度为7900 kg/m3,泊松比为0.285,弹性模量为198 GPa,如表1所示。
对直管型管路、90˚型管路、S型管路、Ω型管路建立模型,如图1所示。
 (a) 直管型管路
(a) 直管型管路  (b) 90˚型管路
(b) 90˚型管路  (c) S型管路
(c) S型管路  (d) Ω型管路
(d) Ω型管路
Figure 1. Finite element models of pipes
图1. 管路有限元模型
其中,各个模型管路的壁厚分别为1.6 mm,1.8 mm,2 mm,2.2 mm,2.4 mm。
3. 仿真分析
3.1. 模态分析
模态分析用于确定管路结构固有频率。根据文献 [15] [16] 关于油压力对固有频率有一定影响,本文采用控制变量法分析不同壁厚和不同管型下对管路固有频率的影响。得到不同管型管路在不同壁厚下的固有频率计算结果,如表2~5所示。


Table 2. Natural frequencies for straight pipelines/Hz
表2. 直管型管路不同壁厚固有频率/Hz

Table 3. Natural frequencies for 90˚ pipelines/Hz
表3. 90˚型管路不同壁厚固有频率/Hz

Table 4. Natural frequencies for S pipelines/Hz
表4. S型管路不同壁厚固有频率/Hz


Table 5. Natural frequencies for Ω pipelines/Hz
表5. Ω型管路不同壁厚固有频率/Hz
由分析结果可知,随着壁厚的逐渐增加,管路的固有频率也逐渐增加。壁厚为1.6 mm的直管型管路、90˚型管路、S型管路、Ω型管路振型图如图2所示。
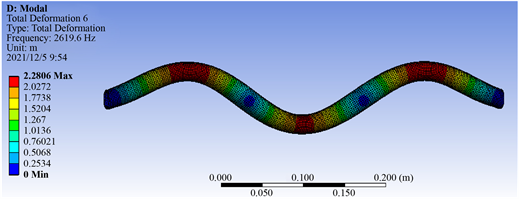 (a) 直管型管路
(a) 直管型管路 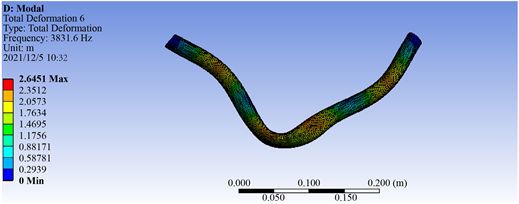 (b) 90˚型管路
(b) 90˚型管路 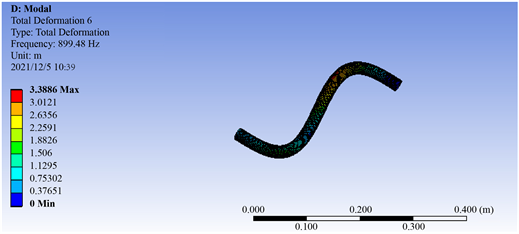 (c) S型管路
(c) S型管路  (d) Ω型管路
(d) Ω型管路
Figure 2. Vibration modes for pipelines
图2. 各管型管路振型图
从以上仿真结果可知,直管管型的变形最小,其次是Ω管型管路、90˚型管路,S管型的变形值最大。
3.2. 振动响应分析
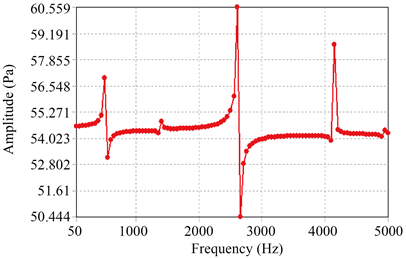
航空发动机管路会受到来自发动机的基础简谐振动激励,正常管道内压力为1~2 MPa [15],根据控制变量法的原则,预应力保持不变,分析管路壁厚为1.6 mm的直管型管路、90˚型管路、S型管路、Ω型管路的振动响应,应力幅值如图3所示。
 (a) 直管型管路
(a) 直管型管路  (b) 90˚型管路
(b) 90˚型管路 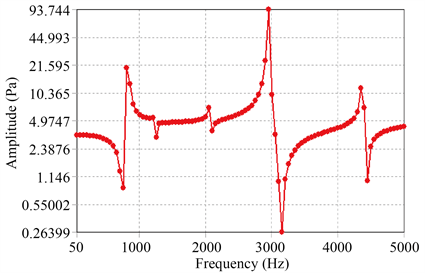 (c) S型管路
(c) S型管路 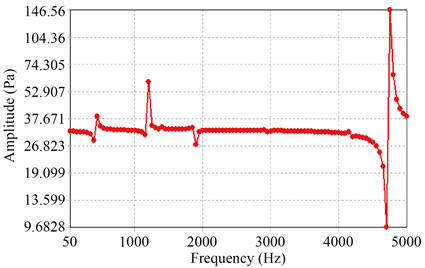 (d) Ω型管路
(d) Ω型管路
Figure 3. Amplitude responses for pipelines
图3. 各管路振动响应幅值图

Table 6. The max stress responses
表6. 应力响应幅值最大值
不同管型管路振动响应值的最大值如表6所示。由振动响应分析结果可知,相同条件下各类管型管路中,直管型管路的应力值最小,其次是S型管路、Ω型管路,90˚型管路应力值最大。
4. 结论
对航空发动机外部管路进行了有限元仿真分析。由分析结果可知,随着管路壁厚的逐渐增加,管路的固有频率逐渐增大。相同条件下各类管型管路振动响应中,直管型管路的应力值最小,其次是S型管路和Ω型管路,90˚型管路振动响应最大。管路设计时应充分考虑管路壁厚和管型对固有频率和振动响应的影响,合理优化设计壁厚和管型,以利于管路的长久稳定工作。
基金项目
NSFC-联合基金“大型复杂机械结构疲劳全寿命可靠性理论及方法研究”(U1708255)。
NOTES
*第一作者。
#通讯作者。