等效配重法在涡扇发动机风扇转子平衡中的应用

Application of Equivalent Counterweight Method in Rotor Balancing of Turbofan Engines

摘要: 为提高某型航空发动机风扇转子动平衡效率，采用等效配重法对风扇转子平衡进行优化。本文以刚性转子叠加系数法为基础，优化风扇转子平衡方法。实验证明优化后方案对提高风扇转子动平衡效率有明显改进。采用该工艺完成的风扇转子已随发动机进行试车检验并通过项目鉴定。

Abstract: In order to improve the dynamic balance efficiency of the fan rotor of aircraft engine, the equivalent counterweight method is used to optimize the fan rotor balance. Based on the rigid rotor superposition coefficient method, this paper optimizes the fan rotor balancing method. Experimental results show that the optimized scheme has significantly improved the dynamic balance efficiency of the fan rotor. The fan rotor completed with this process has been tested with the engine and passed the project qualification.

1. 引言

随着社会的发展，人们对航空发动机的性能提出了越来越高的要求，并使航空发动机最高转速、涡轮前温度等重要参数得到了显著提高。也因此使航空发动机振动故障日益高发。转子零部件材料的不均匀、加工和装配误差 [1]，转静子碰磨，转子不对中，转子连接脱开等都会使发动机运行过程产生振动故障。而发动机转子不平衡引起的振动故障是航空发动机常见并且危害较大的故障 [2] [3] [4]。因此采取有效手段对转子不平衡量进行控制就显得尤为必要。

以某型双转子发动机为例，发动机可分为风扇转子、高压转子、高压涡轮、低压涡轮4大转动部件。而风扇转子是影响航空发动前支点振动的重要部件，也是是航空发动机重要动力来源。其工作性能直接影响发动机振动、推力等重要性能。风扇转子动平衡参数是直接影响发动机振动的主要指标之一。对风扇转子动平衡调节，采用针对刚性转子的影响系数法来测量转子的不平衡量，将转子不平衡量分离成一级转子叶片平面和三级转子叶片平面两个校正平面，在各自校正平面中通过增加材料和材料位移的平衡工艺方法来消除转子的不平衡量。此过程中，因为风扇转子个体间初始不平衡量存在差异，每次平衡时都需参考转子初始不平衡量进行有针对的配重分布和装配。又由于缺乏配重分布后对转子的等效质量的实际数据，往往凭经验进行粗略装配，因此不可避免地需要对配重分布进行多次位移微调。

2. 航空发动机风扇转子平衡技术总体情况

为控制转子初始不平衡量，在转子装配–平衡过程中往往需对各单盘进行静平衡，并对风扇转子叶片测量静力矩。根据各单盘静不平衡量大小及相位，对叶片按静力矩排序实现补偿单盘静不平衡量的目的 [5] [6] [7]。

虽然在装配–平衡过程中已通过跳动检查、控制配合、叶片补偿等方式尽可能提高转子装配质量，但因装配误差等因素存在使转子不平衡量仍超出可接受范围，因此在装配完成后还需对转子组件进行最终平衡。

对转子进行动平衡调节，往往需在两个不同参考平面进行增减质量的操作，从而将转子剩余不平衡量进入可接受范围。某型航空发动机风扇转子动平衡调试就是通过调节一、三级转子轮盘处平衡配重位置和数量实现的。但因可选配重组别有限、转子剩余不平衡量要求高，使得转子动平衡需进行多次“试错”式调节。

3. 主要研究过程

3.1. 方案论证

因风扇转子回转半径大，轴向质量分布较为均匀，因此可将风扇转子简化成两个具有静不平衡的理想刚性转子的组合，而这两个理想刚性转子所在平面及为一、三级轮盘所在平面。因此可分别对上述两刚性转子做静平衡调节，从而实现转子动平衡量控制。

以一级转子叶片平面为例，该平面原始不平量最大允许为U₁ = 700 g∙mm，半径为R₁ = 168 mm，等效成半径处初始质量最大允许为 $M_1=U_1/R_1=4.17\text{g}$ ；剩余不平衡量u₁ = 80 g∙mm，等效成质量为 $m_1=u_1/R_1=476\text{mg}$。

假设一级处转子初始不平衡量为U₁，若消除一级处转子不平衡量，则应在一级轮盘上增加配重，并使增加配重的不平衡量与U₁等大且反向。在实际平衡中，往往因无法提供重量合适的配重，而选取多个配重通过矢量拟合的方式进行不平衡量补偿。

Table 1. Screw quality table at the first and third levels

表1. 一、三级校正平面配重螺钉质量表

如上表1所示，以一级校正平面为例，风扇转子初始不平衡量为0~4.17 g中的某一值，对其进行动平衡调节时，需合理选用配重螺钉，以合理的角度装配到平面内周向分布的螺钉孔内，如图1所示。

Figure 1. Assemble the fan rotor with heavy screws

图1. 对风扇转子装配重螺钉

按照已有的平衡方法，在测得风扇转子一、三级校正平面初始不平衡量后，操作者选取需要组别的配重螺钉并以一定分布方式装配至螺钉孔内。此过程所涉及的配重螺钉组别的选取以及分布方式完全依赖操作者的经验，过程中具有一定不确定性。因此经常需要移动配重位置进行微调，平均每台风扇转子需进行7次微调才能使其剩余不平衡量进入可接受范围。

综上，急需对风扇转子平衡技术进行改进，采取有效措施减少平衡过程中微调次数，并应尽可能提高风扇转子一次平衡合格的成功率

3.2. 方案设计

因风扇转子独特的质量分布，可将其等效成2互不影响的具有静不平衡量的刚性转子。故可分别对前、后校正平面进行静不平衡量调节。

首先对配重螺钉安装位置进行分析。以一级校正平面为例，配重螺钉的安装孔为周向28均匀分布，则相邻两个安装孔的角变化量为 $\theta =360˚÷28=12.86˚$。假设一级校正平面不平衡量为M_i平衡时若以两相同质量m_t的螺钉间隔n个螺钉孔装配(如图2所示)，则可对配重的不平衡量进行矢量计算：

$M_t=2m_t\cos \left(\frac{n+1}{2}\theta \right)$

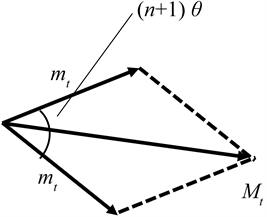
Figure 2. Vector synthesis of counterweights

图2. 配重的矢量合成

若使 $M_t+M_i=0$ 则可使平面内剩余不平衡量为0。综上可根据M_t及配重质量m_t反向求出配重螺钉所需的装配间隔。进一步可求得两个相同组别配重螺钉间隔n个螺钉孔时的等效不平衡量如下表2、表3所示。

Table 2. Equivalent quality of primary counterweight screws

表2. 一级配重螺钉等效质量

Table 3. Equivalent quality of third counterweight screws

表3. 三级配重螺钉等效质量表

在实际平衡中，可参考表2、表3中的数据，合理选用配重并进行装配。具体实施如下：

以一级校正平面为例，假设测得初始不平衡量为1.8 g，60˚。则可选用等效质量最接近1.8 g，或与1.8 g相差在公差范围内的组合如，以2个质量为2.2 g的配重螺钉，间隔10个螺钉孔且以60˚为角平分线装配，则理论上剩余不平衡量为1.8 g − 1.85 g = −50 mg，即50 mg，240˚，使剩余不平衡量进入公差范围。

3.3. 试用

选用9台风扇转子对上述方案进行测试，测试结果如下：

Table 4. The effect of optimization scheme applied in practice

表4. 优化方案在实际平衡中应用效果

由上表4可知，采用优化方案进行风扇转子平衡时，平均每台只需1.3次调节即可，其中一次平衡成功率高达81.8%。

4. 结论

1) 风扇转子因具有较均匀的质量分布，故可将其简化为2具有静不平衡量的刚性转子的组合。在动平衡调节时，前、后校正平面相互影响作用较小，可分别对前后校正平面进行静不平衡调节。

2) 在对转子静平衡调节时，可根据等效质量法，根据配重质量、转子初始不平衡量大小，合理选取配重组别并设置配重装配位置及间隔角度，从而较快地补偿转子初始不平衡量，并使转子剩余不平衡量进入控制范围。