探究惠州市中心城区房价与地价的关系

Exploring the Relationship between House Prices and Land Prices in Huizhou City Center

摘要: 城市房价与地价之间的关系错综复杂，不仅受多种因素的交织影响，相互之间也存在动态关系。研究房价与地价关系的传统，如Granger因果检验和回归分析等，无法刻画房价与地价之间多维网络状关系，相比之下，结构方程模型能同时处理多个内生潜变量，且不受观测指标共线性的影响，为刻画地价与房价的交互作用提供新的工具。从住房与土地市场的供需传导机制出发，推导出房价与地价的结构模型，以惠州市中心城区——惠城区和惠阳区为例，通过2017~2019年居住用地价格和2020年在售和待售楼盘价格，再提取房天下网页中的公共交通可达性，商服繁华度和设施便利度等解释变量，构建地价与房价结构方程模型，分析二者之间的结构关系。

Abstract: The relationship between urban housing prices and land prices is complex, not only affected by the interweaving of many factors, but also dynamic relationships between them. The tradition of studying the relationship between house prices and land prices, such as Granger causality test and regression analysis, cannot describe the multi-dimensional network relationship between house prices and land prices. In contrast, the structural equation model can handle multiple endogenous latent variables at the same time and is not affected by it. Observing the impact of the collinearity of the indicators provides a new tool for describing the interaction between land prices and housing prices. Starting from the supply and demand transmission mechanism of the housing and land markets, the structure model of house prices and land prices is derived. Taking Huizhou’s central urban areas—Huicheng and Huiyang Districts as examples, the prices of residential land in 2017~2019 and those on sale and for sale in 2020 real estate prices, and then extract explanatory variables from the Fangtianxia webpage, such as public transportation accessibility, prosperous business services and facility convenience, construct a structural equation model of land prices and housing prices, and analyze the structural relationship between the two.

1. 引言

近年来，房地产市场的飞速发展，尤其是房价的持续上涨引人注目。除了一线城市的房价不断攀升外，二三线城市也在快速上涨。房价与地价之间的关系一直是研究的热门。目前国内学者大多关注的焦点都在大型城市，而较少关注中小型城市。而常用的研究方法以定量为主，例如通过协整性分析来判断二者是否存在长期稳定的线性关系 [1]；或者通过格兰杰因果检验来探索房价和地价的关系；或是通过回归分析来计算房价与地价之间的影响弹性和贡献程度；以及通过联立方程模型刻画房价与地价的内生关系 [2]，通过事件冲击构建土地出让价格，影响后序住房价格的时序模型。国内学者所得研究结论主要包括，地价的需求增长、价格上涨，从而产生成本转移，促进房价上涨 [3]；从短期来看，房价为因，地价为果，从长期来看，二者相互影响，互为因果等 [4]。

目前研究的局限性在于绝大多数采用简单的数理统计模型来刻画房价和地价的单位关系，但影响地价和房价的因素往往存在一些交织作用，即存在共线性问题，这往往会导致无法甄别房价和地价之间共同影响因子的共变效应以及二者的相互关系。在这一方面，一般的数理统计模型只能刻画房价与地价的单维关系，从而会损失一部分变量之间交互影响的信息。结构方程模型(SEM)能够处理变量间的多维网络状结构关系，克服自变量之间的共线性。因此学者们尝试利用结构方程模型揭示房价与地价间的动态关系，如以北京市为例，揭示影响居住用地价格的因素 [5]；构建北京市别墅的特征价格模型 [6]；揭示重庆市房价与地价的传导关系 [7] [8] 等。考虑到城市房价与地价之间的关系较为复杂，所以试图通过将该模型应用于房价和地价的关系研究中，并以惠州市中心城区，包括惠城区和惠阳区，作为实证分析的案例，构建SEM模型来刻画该地区房价、地价以及各种外部因素之间的多维关系网络，揭示房价与地价的结构关系。

2. 理论依据

土地市场和住房市场存在紧密的供需联动关系：从需求角度来看，对土地的需求是由于人们对住房需求而产生的引致需求，因此房价可以通过需求传导过程影响房价；从供给角度看，土地在住房的成本中占据可观的份额，地价影响住房供给的成本，因此可以通过供给传导过程来影响房价。所以两种价格中任意一种的变动都会导致均衡房价和地价的变动。二者之间存在如图1所示的传导机制：住房需求上升，推升当期房价，同时通过需求传导抬高下一期地价；土地供不应求，提升当期地价，同时通过供给传导抬高下一期房价。“时滞”是作为这一过程的关键。通过从时滞这一动态角度考虑，实际上土地市场与住房市场之间的供需传导不是线性而是环状的 [9]。

Figure 1. Supply and demand chain between house price and land price

图1. 房价与地价之间的供需传导链

3. 模型的推导与构建

3.1. 房价与地价关系的数学推导

“时滞”是房价与地价相互作用的最重要的因素，要研究二者的关系一定要澄清时间起点，如果房价在先，当期房价变动会通过需求传导影响下一期地价；如果地价在先，当期地价会通过供给传导影响下一期房价 [9]。由于房价历史交易信息目前没有公开发布渠道，而相反2017年以来的惠城区和惠阳区的土地出让记录和最新的在售小区信息可以很容易获取，所以采用2017~2019年的地价时间序列数据和2020年房价截面数据作为基础数据集，将土地作为一个房地产运行周期的开端，认为地价先于房价产生，从供给传导的视角出发建立房价与地价关系的模型 [9]。

1) 根据特征价格理论，住房和土地均属于异质性商品，其效用是由一系列属性组合成，如交通条件、基础设施等，因此其需求函数可以表示为一系列属性的函数 [9]：

$H{P}_t^D=F\left(x_1,x_2,x_3,\cdots ,x_i\right)$ (1)

$L{P}_t^D=K\left(y_1+y_2+\cdots +y_i\right)$ (2)

2) 构建住房供给函数：

$H{P}_t^S=H\left(L{P}_{t-1}+C\right)$ (3)

根据住房成本，分解为土地成本和建筑成本、税费等，用LP_t−1表示上一期土地成本，外生变量C表示其他成本。则住房供给函数可表示为一个与地价相关的函数。

3) 当住房市场与土地市场处于长期均衡时，住房需求价格(HPS)等于住房供给价格(HPD)，土地需求价格(LPS)等于土地供给价格(LPD)，且均衡价格水平(HP与LP)长期保持稳定，即 [9]：

$HPS=HPD=HP$ (4)

$LPS=LPD=LP$ (5)

$H{P}_{t=1}=H{P}_{t=2}=\cdots =H{P}_{t=n}$ (6)

$L{P}_{t=1}=L{P}_{t=2}=\cdots =L{P}_{t=n}$ (7)

4) 为了简化模型，认为在一个稳定的房地产经济系统中式(4)~(7)是成立的；且仅考虑交通、邻里、设施等同时影响房价和地价的区位因素，即式(1)~式(2)中 $x_i=y_i$ ；假设与土地成本相比房屋的其他成本C较小可以忽略，函数F、K、H均采用最简单的线性形式。此时式(1)~式(3)可以简化为以下方程组 [1]：

$\{\begin{array}{l}HP={\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_i{x}_i+e(\text{A})\\ LP={\lambda }_1{x}_1+{\lambda }_2{x}_2+\cdots +{\lambda }_i{x}_i+\epsilon (\text{B})\\ HP=\delta LP+\mu (\; C\; )\end{array}$

式中：HP为房价；LP为地价； $x_i\left(i=1,2,\cdots ,n\right)$ 指共同影响房价和地价的外部因素，包括区位、交通、邻里、设施等；其中 ${\beta }_i\left(i=1,2,\cdots ,n\right)$ 表示外部因素对房价影响程度的参数；其中 ${\lambda }_i\left(i=1,2,\cdots ,n\right)$ 表示外部因素对地价影响程度的参数； $\alpha$ 表示地价对房价影响程度的参数； $\epsilon$ 、 $\mu$ 、 $\eta$ 为残差。

3.2. 房价与地价的SEM构建

要对上述的理论模型进行实证检验，就要解决如何刻画变量之间的多维结构关系。之所以选择SEM作为研究的方法，是因为其建模的思想综合因子分析和通径分析，能够处理变量间的多维网络状结构关系，克服自变量之间的共线性。该模型是由测量模型和结构模型两部分组成的 [9]。

1) 测量模型构建

测量模型描述潜变量与观测指标之间的关系，可写作：

$X={\Lambda }_X\zeta +\delta$ (8)

$Y={\Lambda }_Y\eta +\epsilon$ (9)

其中， $\zeta$ 和 $\eta$ 表示为潜变量，如指房价和地价的某个属性，例如交通可达性，但该种属性无法直接观测和量化，所以需要利用交通站的距离和数量以及道路密度等来对多个指标进行估计。而X和Y则是作为可以直接观测的指标。其中 ${\Lambda }_X$ 和 ${\Lambda }_Y$ 因子负荷系数矩阵，指的是观测指标与潜变量之间的关系。 $\delta$ 和 $\epsilon$ 是测量误差矩阵。

SEM中的潜变量包括内生潜变量和外生潜变量，内生潜变量是受到其他潜变量影响的潜变量，相当于因变量；后者则不受其他潜变量影响，仅由观测指标测度的潜变量，相当于自变量。在SEM模型中构地价和房价两个内生潜变量、而区位、交通、基础设施则作为外部要素构成若干的外生潜变量。

2) 结构模型构建

结构模型描述的是各潜变量之间的因果关系。

$\eta =B\eta +\Gamma \zeta +\mu$ (10)

式中： $\eta$ 表示内生潜变量，与一般回归不同的是，结构方程可以包含不止一个因变量，比如房价和地价； $\zeta$ 表示外生潜变量；B为内生潜变量之间的相互影响的路径系数； $\Gamma$ 为外生潜变量对内生潜变量的影响路径系数； $\mu$ 为残差向量。

所构建的结构方程中各潜变量之间存在如图2所示的结构关系，这一模型的意义在于：地价与房价都受到区位、交通、邻里、设施等外部因素的影响，同时上一期地价作为成本的一部分影响当期房价，各潜变量之间的关系分别对应数学推导所得到的三个方程。

Figure 2. SEM diagram of house price and land price

图2. 房价与地价的SEM示意图

3.3. 参数估计方法

结构方程可以通过适当的估计方法估计出各观测指标对潜变量的贡献程度，以及各潜变量之间的路径系数。目前求解SEM主要有两大估计技术，一种是基于极大似然估计的协方差结构分析法，该方法要求变量数据符合联合正太分布假设，且样本量不低于200个，否则所形成的SEM模型是不稳定的，以LISEREL方法为代表 [10]；另一种则是基于最小二乘法的方差分析方法，该方法对样本数据要求没有这么严格，同时适应大容量和小样本。其运行的主要思想是：通过将自变量和因变量的高维数据空间投影到相应的低维空间(整体到局部)，分别得到自变量和因变量的相互正交的特征向量，再建立自变量和因变量的特征向量间的一元线性回归关系。不仅可以克服共线性问题，同时它在选取特征向量时强调自变量对因变量的解释和预测作用，去除了对回归无益噪声的影响，使模型包含最少的变量数 [11]。该方法以PLS方法为代表。

经过ArcGIS中的空间统计分析发现，本文的数据样本并不符合联合正太分布，使用最大似然估计可能会产生偏差。为了达到稳健的估计结果，运用PLS方法对结构方程的参数进行估计。该方法共分为两个步骤：第一步是通过反复迭代得到潜变量估计值；第二步是通过普通最小二乘法进行线性回归，得到测量模型和结构模型的参数估计值。

4. 研究区概况

4.1. 惠城区

惠城区，是惠州市的市辖区，位于广东省东南部，地处粤东地区的交通要津，南临南海大亚湾，与深圳、香港毗邻，惠城区中心坐标为东经114˚40'、北纬23˚08'，总面积1170.6平方公里。

地形地貌方面，地处东江中下游平原区、珠江三角洲东北端。地貌类型多样，台地占6成多，多分布在中部，沿江平原狭小，属东江谷地和西枝江谷地的一部分；平原近3成，多分布在沿江两岸；丘陵不足1成，多分布在北部，以东北－西南走向为主，属粤东岭谷区的一部分。地势为北西南三面向中部倾斜，形成一小盆地。东江水由北而下，到横沥镇后转往西，与西枝江合股后流往博罗。

气候方面，惠城区地处低纬的东江中下游平原区，靠近南海，属南亚热带海洋季风气候，具有春润、夏湿、秋干、冬燥的特点。平均气温为19.5℃~22.5℃，年均降雨量1731毫米，雨量充沛。

交通运输方面，惠城区地处珠江三角洲东北端，东连惠东至汕头280多公里，南往深圳、香港86公里，西往广州130公里，北依罗浮山脉至河源、梅州。大京九铁路、广梅汕铁路、珠三角肇佛广莞惠城际铁路、广汕铁路、赣深铁路以及济广高速、长深高速、武深高速和广龙高速等多条重要快速通道贯穿其中，距惠州港46公里。

4.2. 惠阳区

惠阳区，惠州市下辖区。地处珠三角经济圈东部，东经114˚13'~114˚37'，北纬22˚47'~23˚06'。面积915.6平方公里，下辖淡水、秋长、三和3个街道和沙田、新圩、镇隆、永湖、良井、平潭6个镇，2018年常住人口59.9万，地区生产总值544.14亿元。形成了电子信息、光学玻璃、精细化工、新能源新材料等产业集群，打造了商贸物流、酒店餐饮、休闲旅游、娱乐购物、金融服务全面发展的现代服务业活力区。

地形地貌，区内平原丘陵交错，矮山浅谷广布，山势为东低西高，最高海拔1003.5米，最低为11.0米。

气候方面，惠阳区属南亚热带季风气候，雨量充沛，气候温和，年总雨量为1618.2毫米。全年平均气温在21.1℃~22.2℃之间，年日照时数为2020.6小时，年平均相对湿度78%。

5. 研究方法和思路

本文的研究思路和方法主要分为四个部分，包括：推导地价与房价的函数关系、提取房价和地价数据、利用Smart PLS软件求出待估参数和信度效度检验、对结构进行分析。具体的研究方法如下：

1) 通过对地价和房价关系的数学推导，建立二者的函数关系，以此来初步建立关于SEM的房价与地价模型。2) 通过Python编写脚本，对58同城网中的2020年房价数据以及土地资源网、惠州市公共资源交易中心中的2017~2019年地价数据进行爬取，爬取内容包括两套数据：房价、相应坐标；土地成交价、土地出让面积、土地规划建筑面积、相应坐标。对地价数据进行年限修正，并在Python中对爬取的房地价数据进行坐标转换(BD09- > WGS84)。在这基础上，将修正后的地价数据(2017~2020年)，在ArcGIS中进行克里金插值，形成连续的楼面地价表面。然后，通过ArcGIS的点提取，将楼面地价数据提取至房价数据中；最后，收集各个楼盘2000 m范围内的公交站数量、医院数量、学校数量、1000 m内超市和银行的数量，以此作为外生潜变量的观测指标，最后对所有观测变量进行标准化。3) 通过Smart PLS 3软件绘制各潜变量之间的结构模型，并导入标准化的观测变量，绘制测量模型和结构模型，最终得到结构模型的参数估计结果。再对参数估计结果进行信度和效度检验，包括通过区分效度(Average variance extracted, AVE)、复合信度(Composite reliability, CR)和阿尔法系数(Cronbach’s coefficient alpha, CCA)来进行评价。4) 对估计和检验结果进行分析，得出房价与地价之间的关系。对应的技术路线图，如图3。

Figure 3. Technology road map

图3. 技术路线图

6. 数据来源和数据处理

根据理论模型，最理想的数据样本是有明确的土地出让记录和小区均价记录的楼盘，地价与房价能一一对应，但是这样的数据难以获取，所以试图利用政府多年的出让的住宅用地的数据，运用ArcGIS对地价数据进行空间插值后，将房价和地价样本进行空间定位和匹配。

6.1. 样本提取

基于理论分析，从供给视角分析房价与地价的关系，要确保地价早于房价。因此，基于两个较大的房地产交易网站——58同城(https://huizhou.58.com)和房天下(https://huizhou.fang.com)，选择惠州市的两个中心城区——惠城区和惠阳区，2020年所有在售和待售新房的普通商品住宅小区的均价，一共筛选了185条符合要求的交易记录，作为房价数据样本。而地价数据采用惠州市公共交易中心网站和土地资源网提供的土地出让数据，其中包括2017~2019年通过招标、拍卖、挂牌方式出让的规划用途为居住的152条交易记录。

通过百度地图获取房价样本和地价样本的经纬度坐标，导入ArcGIS，建立点图层，再通过房天下网站收集各个房产样本临近的公园，医院，学校、公交站等数据，并且建立基于GIS平台的空间数据库，如图4。

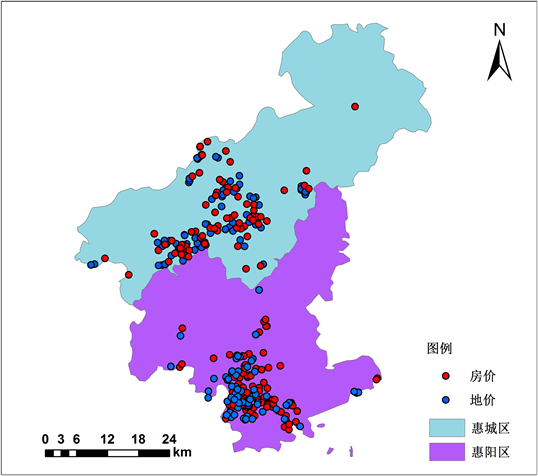
Figure 4. Distribution of house prices and land prices

图4. 房价与地价样点分布图

6.2. 数据预处理

为了得到符合建模需要的数据集，以房价样本为基准，对地价数据样本进行以下的预处理：

1) 根据土地成交价和容积率计算出楼面地价FP。

2) 选择惠州市住宅用地的地价指数作为修正指数对出让期进行修正，剔除样本时间跨度内的通货膨胀、经济增长、房地产市场波动等时间趋势。

3) 将2017~2020年(惠城区样本量N = 85、惠阳区样本量N = 65)地价样本数据分为两组，在ArGIS中通过Spatial Statistics Tools中的空间自相关分析，分析研究区楼面地价的自相关性，通过分析发现惠城区和惠阳区中Z-score > 2.58，表明以99%的置信水平支持楼面地价存在空间自相关这一假设，满足空间插值的前提条件，则再利用Geostatistical Analyst Tools中的普通克里金插值法分别进行空间插值，形成连续的楼面地价表面，插值结果如下图5。

运用ArcGIS对500 m × 500 m的楼面地价栅格通过点提取的方式将地价数据提取至房价样本点的属性表中，从而得到相互匹配的地价与房价数据集。

通过图4和图5都能发现惠城区和惠阳区的房价样点和地价样点的空间分布基本一致，这基本符合出让土地与住宅在空间上一一对应的关系，同时房地价样本点在空间上整体也呈现了聚集的情况，表面其在空间上的分布是会相互影响的，且地价水平是呈块状分布的，这表面地价在空间上是具有一定的相关性的。

Figure 5. Interpolation map of floor price of residential land in Huizhou from 2017 to 2019 ((a) Huicheng District; (b) Huiyang District)

图5. 2017~2019年惠州市住宅用地楼面地价插值图((a) 惠城区；(b) 惠阳区)

7. 模型估计与效果分析

7.1. 模型设计

由于模型包括房价和地价两组内生潜变量，二者均为空间数据，所以其内生地具有空间相关性和空间异质性两种属性，前者意味着距离临近的样本点之间房价(地价)是相互依赖，仅考虑一个个孤立样点的房价和地价关系可能会低估地价对房价的影响程度；后者则认为房价与地价在空间上呈现分异，不仅表现为连续的衰败规律，也包括局部的跳跃和突变，但这对于同一时间截面的房价样本而言，这一属性影响不大，所以就忽略空间异质性的影响，主要考虑空间的相关性 [12]。

因此，通过不同的观测指标设计，拟构建四组SEM模型：

模型1——初始模型，房价与地价潜变量均采用单一观测指标(HP0与FP0)。

模型2——考虑房价与地价的空间的自相关性以及小区(住宅用地)的密度以及小区(住宅用地)的空间距离，对任一样本小区，分别选择其周围最近的3个和6个小区(或住宅用地)样点，按照距离线性衰减的权重计算加权平均值，作为观测指标，构建带有空间滞后属性的房价潜变量和地价潜变量(HP1与FP1)。

各内生潜变量对应的观测指标及其最终进入的模型如表1。

Table 1. SEM Structure of endogenous latent variables

表1. SEM内生潜变量结构表

7.2. 模型估计

基于Hedonic模型的理论基础，并且参考依土地估价和房地产估计的理论以及以往的研究以及数据的可获取性，构建商服繁华度、公共交通可达性、设施便利度等3个外生变量。如表2所示，依次选择了1000 m范围内超市商店数量、1000 m范围内银行数量、2000 m范围内公交站数量、2000 m范围内医院数量、1000 m范围内幼儿园数量、2000 m范围内中小学数量、2000 m范围内大型绿地或公园的数量共7个观测指标分别对3个外生潜变量进行测度，具体的数据通过房天下网站进行收集 [9]。

Table 2. SEM Exogenous latent variables

表2. SEM外生潜变量表

用7个测量指标作为解释变量，房价作为被解释变量利用spss软件进行多元线性回归，建立了一个简单的房价特征价格模型，R² = 0.239，由于变量过多，存在多重共线性的问题，多数的变量不显著，甚至符号与预测相反，如表3。而对于SEM，由于潜变量的存在，可以有效克服观测指标层的共线性问题。

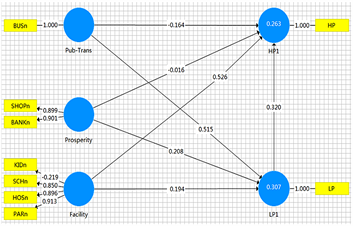
根据研究区的两个内生潜变量和3个外生潜变量来建立初始模型(模型1)，首先运用Smart PLS 3软件绘制各潜变量之间的结构模型图，如图6，然后将惠城区和惠阳区标准化的观测指标数据输入模型，分别得到惠城区和惠阳区结构模型的估计结果如图7(a)和图7(b)，继而改变房价和地价两个内生潜变量，在初始模型的基础上进而构建模型2，惠城区和惠阳区结构模型的估计结果如图7(c)和图7(d)。在SEM的输出结果中，圆圈表示潜变量，方框表示观测变量，连接测量指标与潜变之间的数字为因子负荷系数，反映了各个观测指标与其对应潜变量之间的关系，而连接在潜变量之间的数字为路径系数，反映不同潜变量之间影响程度，箭头方向表示影响施加的方向。

Table 3. Multiple linear regression analysis

表3. 多元线性回归分析

Figure 6. SEM structure of model 1

图6. 模型1的SEM结构图

(a) Model1 (b) Model1 (c) Model2 (d) Model2

Figure 7. SEM Parameter estimation results ((a), (c) on behalf of Huicheng District, (b), (d) on behalf of Huiyang District)

图7. SEM参数估计结果((a)、(c)代表惠城区，(b)、(d)代表惠阳区)

7.3. 测量模型效果评测

测量模型将观测指标与潜变量之间通过因子负荷系数建立联系，通过对惠城区和惠阳区各两个模型的计算结果的观察发现，虽然惠城区与惠阳区的模型计算结果有所不同，但是其大部分的观测指标的因子负荷系数都高于0.9，这就意味着从总体来看，观测指标对潜变量的解释程度较好。

测量模型的信度和效度可以通过区分效度(Average variance extracted, AVE)、复合信度(Composite reliability, CR)和阿尔法系数(Cronbach’s coefficient alpha, CCA)来进行评价 [9]，如表4。其中AVE是检验各潜变量之间相互区分的程度，这一数值表示用潜变量的方差解释相应的观测变量方差的百分比，即检验该潜变量对应的观测变量解释的有效性。惠城区和惠阳区的2个模型中，惠城区的两个模型的AVE值均大于0.5，而惠阳区的两个模型AVE值大部分大于0.5，这表明从总体上各个构面的区分的效果较好，而惠阳区可能存在小部分构面重叠；CR检测观测指标是否能一致地测度对应的潜变量，结果发现惠城区的两个模型的效果更好，CR基本均大于0.8，而惠阳区中的设施便利度这个外生潜变量的CR值只有0.49，这说明该观测指标对地价的影响存在不一致现象，且差距较大，这通过图7就能发现，中小学数量和医院数量的因子负荷系数远小于幼儿园和绿地数量；α系数CCA是评估观测变量能够解释其所构建的潜变量的程度，通常认为，当α系数的值大与0.7时，所构建的测量模型具有满意的信度和稳定性，而所构建的模型基本达到了这一标准。

7.4. 结构模型效果评测

结构模型模拟的是3个外生潜变量和2个内生潜变量的关系，评测参数主要包括路径系数和拟合优度。路径系数反应出潜变量之间作用强度，如表5。在惠城区中，对房价有显著作用的潜变量是公共交通可达性和设施便利度，其影响都为正向，而对楼面地价有显著影响作用的潜变量包括公共交通可达性、商服繁华度和设施便利度，影响均为正向。而在惠阳区中，对房价有显著作用的潜变量是公共交通可达性，影响为正向，而对楼面地价有显著影响的潜变量是公共交通可达性和设施便利度，影响均为正向。

Table 4. SEM Measurement model parameters

表4. SEM测量模型参数

Table 5. SEM Structural model parameters

表5. SEM结构模型参数

R²表示的是构建模型的拟合程度和对外生潜变量的解释程度，当R² = 0.33左右表示具有中度解释能力，当R² > 0.67表示解释能力较好。而从表6可以看出，所构建的模型普遍对地价的解释能力较强，基本达到了0.5，但是对房价的解释能力为中等。这表明所选取的外生潜变量对地价的拟合度或是解释能力比房价更高，同时发现，由于模型2考虑了房价和地价的空间相关性，所以模型2拟合情况有所改善，这表明无论房价和地价，其在空间中并不是孤立存在的，在一定的距离范围内是存在相互影响，而这主要是因为其所处的区位存在相似性和可比性。

Table 6. SEM Structural model goodness of fit

表6. SEM结构模型拟合优度

8. 结果分析

8.1. 房价与地价的结构关系

从SEM的估计结果可以看出，各个区位因子对房价和地价的作用是不同的，有的单独作用于地价和房价之一，有的同时作用于二者，据此将影响房价与地价的潜变量可分为两类，以惠城区为例：1) 对地价影响显著而对房价影响不显著，包括：商服繁华度，其对楼面地价的直接影响为0.208，而对地价的影响为0.016；2) 对房价和地价作用均为显著的是公共交通可达性和设施便利度，公共交通可达性单独对房价的影响0.164~0.167和对地价直接影响为0.515，而设施便利度对房价的影响为0.526~0.533，对地价的影响为0.194；3) 地价和房价存在显著影响，影响系数大约为0.32~0.384。综上所述，惠城区地价与房价的结构示意图，如图8。

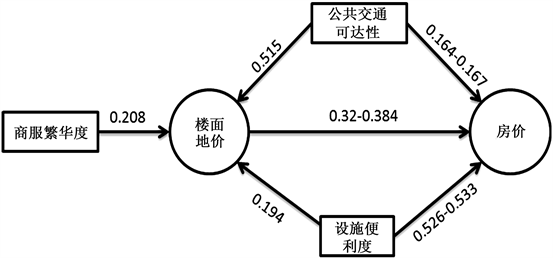
Figure 8. Relationship between land price and house price

图8. 楼面地价与房价关系图

为什么会出现不同区位因子对房价和地价的影响不同？这一结果可以从两个方面解释：1) 从理论角度来看，很可能源于土地出让环节和住房环节中不同主体对各项因素的权重排序不同，有些因素是土地出让时开发商更多考虑的加分项，有些因素是买卖房产时买房者更多考虑的加分项，而观测指标的选取也是极其重要，虽然不同的地区对房价和地价的影响因素大多相同，但是由于不同地区的经济发展状况不同，所以产生的需求就会不同，而影响因素也会存在差别，因此指标的补充和筛除会直接影响外生潜变量对内生潜变量的影响程度。2) 从方法角度来看，结构方程的潜变量层能起到“聚类”的作用，通常研究中，超市商店、银行、幼儿园、小学、医院、公园被认为是平行的生活便利设施，但是从惠城区实际分布来看，超市商店与银行相对普遍，而幼儿园、小学、医院和公园相对稀缺，前者的密度往往代表着人流的多少、地段的好坏，是开发商买地时更多考虑的因素，而后者的远近和数量往往代表着生活质量的高低，是买房者更多考虑的因素。所以通过SEM可以揭示同一类指标对不同因变量的传导关系。

而更进一步解释地价与房价的结果关系，可以认为一部分区位因子是通过供给端影响房价，一部分区位因子是通过需求端影响房价。根据理论模型推导中相关分析，住房均衡价格可能因为供给和需求任意一端的波动而抬高，对于一个城市，其房价可看作是受成本和相对稀缺度两个部分影响。就本研究中选取的影响因素而言，可以认为商服繁华度变量更多是通过影响土地需求函数来影响地价，进而通过供给端将成本转移于房价上，而公共交通可达性和设施便利度则可以直接影响房价需求函数，从而影响房价。

8.2. 地价对房价的影响程度

模型1在没有考虑空间相关性的情况下，估测出地价对房价影响的路径系数为0.32，这与纳入了空间滞后的模型2相比，这一系数应该是低估了地价和房价的影响。模型2的估测结果为0.384，且二者均在p = 0.05水平上显著，因此可以推算出惠州市惠城区地价对房价的路径系数大约为0.32~0.384。这也就意味着地价有显著影响的因素，可以通过大致为0.32~0.384的路径系数传导给房价。以公共交通可达性为例，其对房价的影响为0.165左右，对地价的影响为0.515，通过地价对房价施加的间接的影响为0.15~0.2左右，所以公共交通可达性对房价的总影响为0.21~0.37。而商服繁华度虽对房价没有显著直接影响的变量，但也通过地价的成本传导机制对房价产生一定的正向影响。

9. 结论和不足

9.1. 结论

从土地市场与住房市场之间的供给需求传导关系入手，通过理论分析推导出刻画房价和地价关系的模型，选择SEM作为研究方法，以惠州市惠城区和惠阳区作为实证分析案例，刻画房价、地价和各种外部因素之间的多维关系结构，主要得出如下结论：

1) 土地市场与住房市场之间通过供给和需求紧密联系，当期房价的上涨可以通过需求传导拉动下一期地价，当期地价的上涨也可以通过供给传导推升下一期房价。实证分析的结果表明，惠州市惠城区和惠阳区2020年房价受2017~2019年住宅用地的出让价格显著影响，影响方向为正，这验证了往期地价对当期房价存在推动作用。并且当综合考虑了房价和地价的空间相关性后，这一影响的估计值变大，根据SEM估计结果，推导出惠州市中心城区地价对房价的影响的路径系数大致为0.3~0.38。

2) 区位因子对地价和房价的作用多样化，有的对地价显著，有的同时对地价和房价具有显著影响。而这一现象的原因是由于部分区位因素主要是通过供给端影响房价，部分因素是通过需求端影响房价。根据SEM估计结果，在惠城区房地产市场中，商服繁华度更多地是通过影响土地需求函数来影响地价，从而通过影响成本来影响房价。而公共交通可达性和设施便利度则可以直接影响住房需求函数，来影响房价。

9.2. 不足

限于数据可得性，在房价与地价样本的匹配过程中采用了空间插值和点数据提取，尽管地价样本较大且插值误差较小，但数据的准确性仍然受到了影响，并且在实证模型中无法纳人绿化率、容积率、产权年限等社区自身属性变量，可能会影响到模型参数估计的准确性。未来随着房地产市场数据逐渐开放，若能够追踪到具体楼盘的出让地价、出售房价和更多微观信息，将有可能对本文的模型进行进一步修正和改善。

参考文献